Pi, nombre univers

[moijesuissansE]

Bonjour,
Je suis en terminale et ai une question pour mon grand oral : tout l'univers est-il contenu dans pi ?
Ce sujet me passionne vraiment et je souhaite travailler dessus, en abordant la thématique des nombres univers...
Sauriez vous comment puis-je relier ce sujet au programme de maths de première et de terminale svp, j'ai vraiment besoin d'aide...

Merci par avance


Programme comportant entre autres, géométrie dans l'espace, probabilités, variables aléatoires, dénombrement, trigonométrie, raisonnement par récurrence, suites fonctions et leurs limites....ou encore le programme de maths expertes : nombres complexes, nombres premiers, graphes, matrices.....

[moijesuissansE]

En fait mon prof de maths est parti en vacances et je n'ai personne a qui poser la question...

[GaBuZoMeu]

Bonjour,

On ne sait même pas si le développement décimal de contient par exemple un nombre infini de (ce qui est beaucoup plus faible que d'être un nombre univers).
Tu peux voir les pages wikipedia sur nombre univers, nombre normal.
Tout le monde pense que est un nombre normal, mais personne ne sait le démontrer.
On peut faire des expériences en python sur la fréquence d'apparition des différentes suites de 3 chiffres dans le premier million de décimales de ...

[moijesuissansE]

Merci pour votre réponse !
Oui, il est vrai que jamais il n'a été démontré quelconque propriété de ce type pour pi....
Concernant le programme python, il suffirait donc d'expliquer que, si pi est normal, chaque fréquence d'apparition de suite de 3 chiffres vaut 1/1000 ?

[GaBuZoMeu]

Je dirais plutôt "est proche de 1/1000".

[moijesuissansE]

D'accord merci beaucoup, j'espère que au milieu de tout mon argumentaire ça suffira pour être considéré en lien avec le programme....

[GaBuZoMeu]

Tu peux regarder la répartition des nombres d'occurrences trouvés pour les 1000 suites possibles de trois chiffres dans le premier million ou les deux premiers millions de décimales de . Tu peux calculer la variance de cette série, comparer avec la variance d'une variable aléatoire comptant le nombre de succès dans une suite de tirages avec probabilité de réussite 1/1000. Tu peux aussi renouveler l'expérience avec d'autres constantes comme 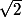ou etc.

[moijesuissansE]

Ok je vois, ça m'aide beaucoup, vraiment merci !
Sauriez vous où je peux trouver un fichier contenant le plus de décimales de pi possible ?

[GaBuZoMeu]

Fais une recherche avec "million digits of pi" et tu trouveras ton bonheur. On peut même télécharger un fichier .txt avec un milliard de décimales (ça prend un peu de temps !).

[moijesuissansE]

Ok parfait, merci infiniment vous me sauvez !