Bonjour, j'ai besoin d'aide!
Notre prof de maths nous propose des petits DM bonus pour la moyenne!
Voici le sujet de ce nouveau DM:
Trouver un problème dont la solution demande de résoudre l'équation : x² - x - 1 = 0
Nous avons commencé à étudier en cours le nombre d'or, mais je n'ai pas tout compris. Alors de quoi proposer un sujet de problème!
J'ai mis que x² = x+1
Mais après...
Merci si quelqu'un peut m'orienter.
Le nombre d'or
9 messages
- Page 1 sur 1
Bonjour,
le nombre d'or ne fait que l'objet d'exercices, exercices corrigés en cours tu veux dire ...
eh bien déja tu as vu la définition du nombre d'or ?
et ce n'est pas "par définition le nombre d'or est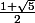 "
"
mais "par définition le nombre d'or est le rapport des dimensions d'un rectangle etc ..."
donc ça te donne déja un énoncé de problème dont la solution s'obtient en résolvant cette équation !
les nombreuses propriétés géométriques du nombre d'or t'en donnent d'autres :
- partage d'un segment en moyenne et extrême raison
c'est à dire étant donné un segment AB trouver le point M de AB tel que le rapport de AM/AB soit égal au rapport de MB/MA
- trouver le rapport entre les diagonales d'un pentagone régulier et son coté
etc ...
tu peux aussi "traduire" l'équation x² = x+1 en considérant des problèmes algébriques
trouver un nombre qui augmenté de 1 donne son carré (traduction mot à mot de cette équation !)
ou trouver un nombre qui surpasse son inverse de 1
trouver deux nombres dont le produit est 1 et la différence 1
etc ...
un cours sur le nombre d'or ??kikis a écrit:étudier en cours le nombre d'or
le nombre d'or ne fait que l'objet d'exercices, exercices corrigés en cours tu veux dire ...
eh bien déja tu as vu la définition du nombre d'or ?
et ce n'est pas "par définition le nombre d'or est
mais "par définition le nombre d'or est le rapport des dimensions d'un rectangle etc ..."
donc ça te donne déja un énoncé de problème dont la solution s'obtient en résolvant cette équation !
les nombreuses propriétés géométriques du nombre d'or t'en donnent d'autres :
- partage d'un segment en moyenne et extrême raison
c'est à dire étant donné un segment AB trouver le point M de AB tel que le rapport de AM/AB soit égal au rapport de MB/MA
- trouver le rapport entre les diagonales d'un pentagone régulier et son coté
etc ...
tu peux aussi "traduire" l'équation x² = x+1 en considérant des problèmes algébriques
trouver un nombre qui augmenté de 1 donne son carré (traduction mot à mot de cette équation !)
ou trouver un nombre qui surpasse son inverse de 1
trouver deux nombres dont le produit est 1 et la différence 1
etc ...
mais partir de la suite de Fibonacci pour en déduire que cette suitemathelot a écrit:bonjour,
donner une écriture de la suite de Fibonacci
avec le nombre d'or.
alors c'est vrai que kikis ne précise pas quel est le niveau, mais on peut penser que c'est plutôt seconde / première que Terminale !!
(mes exemples se situaient à ce niveau)
kikis a écrit:Merci beaucoup: voici l'énoncé que j'ai choisi :
Pierre choisit un nombre qui vérifie la propriété suivante : « Si jajoute 1 à ce nombre, on obtient son carré ».
Quel est ce nombre ?
C'est vraiment bien ce forum!
Ton idée est intéressante. Il y a plein d'autres options, c'est ça qui est chouette. Par exemple :
* trouver deux nombre dont la somme est 1 et le produit -1
* si j'enlève 1 à ce nombre, j'obtient son inverse
* (classique) trouver deux nombres a et b tels que
salut
soit d le nombre d'or :
1/ comparer d² et d.
2/ existe-t-il un autre nombre vérifiant la même propriété ?
3/ si oui comparer alors ces deux nombres ....
pour "faire du numérique" et des fonctions ....
soit c la fonction carré et g la fonction x --> x + 1., et C et D leur courbe représentative.
1/ à l'aide de la calculatrice donner une valeur approchée des abscisses des points d'intersection de C et D.
2/ déterminer la valeur exacte de ces nombres ...
3/ calculer la somme, leur produit et leur quotient ....
idem en considérant les fonctions inverse h et g : x --> x - 1
....
:zen:
soit d le nombre d'or :
1/ comparer d² et d.
2/ existe-t-il un autre nombre vérifiant la même propriété ?
3/ si oui comparer alors ces deux nombres ....
pour "faire du numérique" et des fonctions ....
soit c la fonction carré et g la fonction x --> x + 1., et C et D leur courbe représentative.
1/ à l'aide de la calculatrice donner une valeur approchée des abscisses des points d'intersection de C et D.
2/ déterminer la valeur exacte de ces nombres ...
3/ calculer la somme, leur produit et leur quotient ....
idem en considérant les fonctions inverse h et g : x --> x - 1
....
:zen:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Bonjour,

Puis-je permettre de soumettre ma contribution.
Soit un nombre .
.
Construisons un rectangle ABCD tel que AB=1 et ...
...
Et je recherche quelle peut bien être la valeur de si j'impose la condition suivante :
si j'impose la condition suivante :
Soient E et F appartenant respectivement à [AD] et [BC], tels que (EF)//((AB) et AE=1...
ABFE est un carré de côté 1, EFCD est un rectangle de longueur 1 et largeur
Quelle doit être la valeur de \phi pour que le rapport reste égal à
reste égal à  ?
?
 qui ramène à la résolution de
qui ramène à la résolution de 
Soient G et H appartenant respectivement à [EF] et [DC] tels que (GH)//(AD) et GF=FC...
FGHC un est un carré de côté et GEDH un rectangle de longueur
et GEDH un rectangle de longueur  et de largeur
et de largeur =2-\phi)
Le rapport Longueur/largeur de ce rectangle est-il resté le même ?
 et on retombe sur l'équation précédente...
et on retombe sur l'équation précédente...
Et on peut continuer en construisant un carré DHIJ dans le rectangle EDHG... le rapport Longueur/largeur reste constant...
Cerise sur le gâteau, mais ce n'est plus du niveau de kikis, par les points A, F, H, Jn l, N... passe une spirale logarithmique...
Il y a longtemps avec le BASIC de l'Amstrad CPC 6128, j'avais réalisé cet emboîtement et tracé la spirale, à la précision de l'écran près...
Bye

Puis-je permettre de soumettre ma contribution.
Soit un nombre
Construisons un rectangle ABCD tel que AB=1 et
Et je recherche quelle peut bien être la valeur de
Soient E et F appartenant respectivement à [AD] et [BC], tels que (EF)//((AB) et AE=1...
ABFE est un carré de côté 1, EFCD est un rectangle de longueur 1 et largeur
Quelle doit être la valeur de \phi pour que le rapport
Soient G et H appartenant respectivement à [EF] et [DC] tels que (GH)//(AD) et GF=FC...
FGHC un est un carré de côté
Le rapport Longueur/largeur de ce rectangle est-il resté le même ?
Et on peut continuer en construisant un carré DHIJ dans le rectangle EDHG... le rapport Longueur/largeur reste constant...
Cerise sur le gâteau, mais ce n'est plus du niveau de kikis, par les points A, F, H, Jn l, N... passe une spirale logarithmique...
Il y a longtemps avec le BASIC de l'Amstrad CPC 6128, j'avais réalisé cet emboîtement et tracé la spirale, à la précision de l'écran près...
Bye
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
