Nombre de diviseurs

[beagle]

1 à 42
attention Anthony, l'humain est un animal apprenant, et les maths l'art de ne pas avoir à calculer.
Donc de ce fil on pourrait tirer par exemple:
De l'ami nodjim:
les diviseurs avec du 5, ils vont bien jusqu'à 5x9 =45
donc on a 1,2,3,4,5,6, 8 cela fait 7

les diviseurs sans le 5:
8x9= 72 à enlever mais le reste est inf à 42 (le 8x3 et le 4x9 déjà inf)
donc on prends tous les diviseurs avec 2 et 3
4 pour le 2 fois 3 pour le 3 = 4x3 =12
on enlève 1, 12-1 =11

11+7 =18 ? C'est-y ça?

[zygomatique]

je ne comprend spas comment dénombrer dans [0, 125] est plus difficile que dans [0, 200]

facile

Un dénombrement efficace en terme de temps consiste (ruse du flemmard) à calculer le nombre de diviseur total (facile) et à retrancher ceux qui sortent de l'intervalle mais lorsque l'intervalle contient autant ou moins de diviseurs qu'en dehors de l'intervalle alors le dénombrement est plus long. Vous nous proposez la valeur et c'était mon intuition également mais je n'ai toutefois pas réfléchi à une preuve en bonne et due forme de ce résultat (c'était par instinct).
Pour revenir sur le nombre de diviseurs de , le dénombrement le plus long (en terme de temps pour un humain avec une feuille et un crayon) aurait été de trouver tous les diviseurs de appartenant à l'intervalle plus que ou .

c'est un exo que je donne à mes élèves de term spé math en DM ...

soit n = pq (on travaille dans N)

montrer que .

généralisation :

à toi de jouer ...

(la démo tient en une ligne et deux équivalences)

[anthony_unac]

Bonjour,

Je ne vois pas le lien entre votre exercice et le fait qu'un nombre (ayant un nombre total de diviseurs pairs) donné possède autant de diviseurs dans l'intervalle qu'en dehors de cet intervalle ?! Dans votre exercice, tout se passe comme si avait précisément 4 diviseurs : 1;p;q et p.q
J'ai du loupé un truc quelquepart !

PS : Posons pour trois entiers naturels , et l'égalité :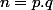
Si alors mais , l'inéquation devient alors :
autrement dit

[zygomatique]

je ne vois pas ce que viens faire la parité du nombre de diviseurs ni même le nombre de diviseurs ...

je dis simplement que si j'écris n comme un produit de deux entiers alors on a ce que je demande de montrer :

c'est un exo que je donne à mes élèves de term spé math en DM ...

soit n = pq (on travaille dans N)

montrer que .

généralisation :

à toi de jouer ...

(la démo tient en une ligne et deux équivalences)

[nodgim]

@ Zygomatique:
Pour tes élèves de Terminale, un peu plus corsé:
Soit les nombres de la forme 4n² + 1. Si pour n = a, on a une décomposition en facteurs premiers 4a² + 1 = p*q*r*s, combien, parmi ces 4 facteurs premiers distincts, y en a t'il qui apparaissent au moins une fois dans la décomposition des nombres 4n²+1 pour n < a ?

Bon amusement