Bonsoir
je m'initie au nombre complexe tout aller bien, jusqu'à la transformation en forme trigonométrique.
Je suis complément perdu.
Voici un cercle de trigonométrique, comment puis je l'utiliser pour la transformation complexe en forme trigonométrique.
<a href="https://www.casimages.com/i/181023092109872308.jpg.html" title="cercletrigonometrique">Lien vers mon image</a>
A bientôt
Nombre complexe et cercle trigonomêtrique
3 messages
- Page 1 sur 1
Re: Nombre complexe et cercle trigonomêtrique
par pascal16 » 23 Oct 2018, 20:18
Il est pas très lisible
en abscisse les cosinus, en ordonnée les sinus.
exp(i pi/3) a pour cosinus 1/2 et sinus V3/2 soit "1/2 + i V3/2"
en abscisse les cosinus, en ordonnée les sinus.
exp(i pi/3) a pour cosinus 1/2 et sinus V3/2 soit "1/2 + i V3/2"
Re: Nombre complexe et cercle trigonomêtrique
par mathelot » 23 Oct 2018, 21:01
bonsoir,
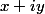est l'affixe d'un point M(x;y) du plan.
On peut passer en coordonnées polaires)
par les formules
)
)
Ces formules s'inversent:
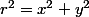
=\dfrac{y}{x})
)
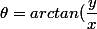si x>0
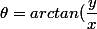+\pi)
si x<0
=\dfrac{x}{\sqrt{x^2+y^2}})
=\dfrac{y}{\sqrt{x^2+y^2}})
on obtient donc
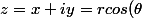+i r \sin(\theta)=r(cos(\theta)+i \sin(\theta)))
on pose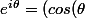+i \sin(\theta)))
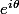est un complexe de module 1
On peut passer en coordonnées polaires
Ces formules s'inversent:
on obtient donc
on pose
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :