:help: Exercice .
1) Déterminer les racines carrées de chaque nombre complexe : a) 24 +70 i b) 2 2 i .
2) Résoudre dans C l'équations suivante : a) z²+(4+2i)z+6+8i
je suis bloquer je sais même pas comment faire quelque peut m'expliquer en détaille comment faire svp merci
Nombre complexe aide
7 messages
- Page 1 sur 1
par zygomatique » 11 Fév 2015, 18:33
salut
on pose z = x + iy
on calcule son carré
on identifie avec 24 + 70i (ou avec 2 - 2i)
...
on pose z = x + iy
on calcule son carré
on identifie avec 24 + 70i (ou avec 2 - 2i)
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
par chombier » 11 Fév 2015, 20:54
zygomatique a écrit:salut
on pose z = x + iy
on calcule son carré
on identifie avec 24 + 70i (ou avec 2 - 2i)
...
Il y a une astuce en plus sinon on se retrouve avec deux équations qui ne sont vraiment pas agréables:
(Je ne vois pas trop comment résoudre ce système personnellement, même si c'est surement faisable)
L'astuce consiste à dire que si
Avec les trois équations :
Cela devient presque facile
par zygomatique » 11 Fév 2015, 21:08
misère ... 
pourquoi tout donner gratuitement .... :mur:
24 = 1 * 24 = 2 * 12 = 3 * 8 = 4 * 6
35 = 1 * 35 = 5 * 7
ho comme c'est marrant ::
5 + 7 = 12
7 - 5 = 2
:ptdr:
pourquoi tout donner gratuitement .... :mur: 24 = 1 * 24 = 2 * 12 = 3 * 8 = 4 * 6
35 = 1 * 35 = 5 * 7
ho comme c'est marrant ::
5 + 7 = 12
7 - 5 = 2
:ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
par paquito » 12 Fév 2015, 15:07
zygomatique te propose une solution originale! Plus rigoureusement on calcule (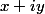^2=x^2-y^2)
; d'où le système:
1x^2-y^2=24)
2)
3)
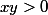
de 1) et 2) on tire facilement
et
et comme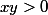 les 2 racines sont :
et 
. Cette méthode est très classique et efficace. L'astuce de zygomatique est difficile à utiliser pour chercher les racines carrées de
.
1
2)
3)
de 1) et 2) on tire facilement
par zygomatique » 12 Fév 2015, 16:27
abs est la valeur absolue ...
oui bien sur "ma" méthode repose sur le fait que les solutions ne sont pas "compliquées" ....
je factorise par 4 et ne m'occupe que de
(*) évidemment tout le monde connaît les carrés de 1 + i et 1 - i (ça s'appelle l'expérience et le travail manuel :lol3: ) donc
 = (a + ib \sqrt 5)^2 = a^2 - 5b^2 + 2abi \sqrt 5)
donc
donc
équation bicarrée qui se résout sans aucune difficulté ....
et comme tout le monde connaît les racines carrés de i (d'après (*)) c'est fini ...
pour revenir à
alors
en remplaçant x² dans la deuxième on obtient une équation bicarrée qui permet de déterminer y puis x
évidemment élever au carré conduit à une implication et non pas une équivalence ... il faut donc vérifier les solutions ....
cette méthode permet de se passer du module ... mais bon quand l'idée du module est connue c'est tout de même beaucoup plus simple ...
:lol3:
oui bien sur "ma" méthode repose sur le fait que les solutions ne sont pas "compliquées" ....
je factorise par 4 et ne m'occupe que de
(*) évidemment tout le monde connaît les carrés de 1 + i et 1 - i (ça s'appelle l'expérience et le travail manuel :lol3: ) donc
donc
donc
équation bicarrée qui se résout sans aucune difficulté ....
et comme tout le monde connaît les racines carrés de i (d'après (*)) c'est fini ...
pour revenir à
alors
en remplaçant x² dans la deuxième on obtient une équation bicarrée qui permet de déterminer y puis x
évidemment élever au carré conduit à une implication et non pas une équivalence ... il faut donc vérifier les solutions ....
cette méthode permet de se passer du module ... mais bon quand l'idée du module est connue c'est tout de même beaucoup plus simple ...
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :