Nbr complexes ! svp
17 messages
- Page 1 sur 1
nbr complexes ! svp
Bonjour,
Voila j'ai un exo à faire mais je bloque sur quelques questions
On se place sur le plan complexe.
On appelle f l'application qui à tout point M d'affixe z associe le point M' d'affixe z' tel que : f(z) = z' = z²+1
1)
a) Montrer que f admet deux invariants dont on précisera les affixes
j'ai utiliser le discriminant et je trouve z1 = i et z2 = -i
b) Expliquer pourquoi f n'st ni une translation, ni une rotation, ni une homothétie.
je n'y arrive pas :s
2) Montrer que deux point symétrique par rapport à O on même image
ça c'est bon je l'ai fait
3) Soit A le point d'affixe : za = V2/2 +V2/2i. A' est son image par f.
a) déterminer l'affixe du point A'
c'set bon je trouve zA' = 1+i
b) Montrer que O, A et A' sont alignés.
Je n'y arrive pa Je Bloque ! :s
4) Soit ;) appartenant à [0 ; 2;) ] Soit N le point d'affixe zN = e(itéta). Soit N' son image par f.
a) En utilisant les formules d'Euler, montrer que zN' = 2cos;)zN
b) En déduire que O, N et N' sont alignés
Tout la question 4 je n'y arrive pas :s je bloque aussi
Merci d'avance !!
Voila j'ai un exo à faire mais je bloque sur quelques questions
On se place sur le plan complexe.
On appelle f l'application qui à tout point M d'affixe z associe le point M' d'affixe z' tel que : f(z) = z' = z²+1
1)
a) Montrer que f admet deux invariants dont on précisera les affixes
j'ai utiliser le discriminant et je trouve z1 = i et z2 = -i
b) Expliquer pourquoi f n'st ni une translation, ni une rotation, ni une homothétie.
je n'y arrive pas :s
2) Montrer que deux point symétrique par rapport à O on même image
ça c'est bon je l'ai fait
3) Soit A le point d'affixe : za = V2/2 +V2/2i. A' est son image par f.
a) déterminer l'affixe du point A'
c'set bon je trouve zA' = 1+i
b) Montrer que O, A et A' sont alignés.
Je n'y arrive pa Je Bloque ! :s
4) Soit ;) appartenant à [0 ; 2;) ] Soit N le point d'affixe zN = e(itéta). Soit N' son image par f.
a) En utilisant les formules d'Euler, montrer que zN' = 2cos;)zN
b) En déduire que O, N et N' sont alignés
Tout la question 4 je n'y arrive pas :s je bloque aussi
Merci d'avance !!
1 a) Bon tu commence mal : qu'est-ce qu'un invariant ? c'est f(z) = ...
b) quel est la forme d'une rotation ? d'une homotéthie ? d'une rotation ? ou encore sais-tu ce que préserve ces transformations ? Est-ce le cas pour celle que tu étudies ?
3) pour montrer que des points sont alignées une bonne idée est de montrer que les vecteurs sont colinéaires, donc que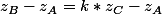 où k est réel. Ou encore que le quotient appartient à
où k est réel. Ou encore que le quotient appartient à 
4a) et bien calcule l'affixe N' en remplaçant z par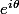
b) je t'ai dit comment faire plus haut
Revient poser des questions si tu n'y arrive pas...
b) quel est la forme d'une rotation ? d'une homotéthie ? d'une rotation ? ou encore sais-tu ce que préserve ces transformations ? Est-ce le cas pour celle que tu étudies ?
3) pour montrer que des points sont alignées une bonne idée est de montrer que les vecteurs sont colinéaires, donc que
4a) et bien calcule l'affixe N' en remplaçant z par
b) je t'ai dit comment faire plus haut
Revient poser des questions si tu n'y arrive pas...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
1a) un point fixe est un point qui n'est pas modifié par la transformation donc f(z) = z.
b) Et non z² ne conserve pas les longueurs (regarde sur la droite réelle par exemple)... Il suffit de le montrer sur un exemple (par exemple la distance entre 0 et 1)
4 a) et après regarde ce qu'il faut obtenir... tu dois avoir qqchose * zN, donc factorise par z_N.
b) Et non z² ne conserve pas les longueurs (regarde sur la droite réelle par exemple)... Il suffit de le montrer sur un exemple (par exemple la distance entre 0 et 1)
4 a) et après regarde ce qu'il faut obtenir... tu dois avoir qqchose * zN, donc factorise par z_N.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
1a) tu te compliques la vie : tu as un trinome dont tu cherche les racines !
1b) et ben tu calcules l'image de 0 et l'image de 1, tu calcule leur distance et tu vois que c'est différent de celle des points d'origine... ou pas. Alors tu essaies avec 0 et 2...
1b) et ben tu calcules l'image de 0 et l'image de 1, tu calcule leur distance et tu vois que c'est différent de celle des points d'origine... ou pas. Alors tu essaies avec 0 et 2...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
C'est pourtant une "astuce" des plus classiques et des plus efficaces : quand tu veux montrer une égalité, montre que la différence est nulle ! Car tu as plein de résultats / formule pour trouver les racines d'une fonction (ce qui est en fait assez général puisque cela te permet de montrer une égalité quelconque...)
Pour ta culture et piquer ta curiosité : quand tu seras grand, si tu fais un jour des maths (bon d'accord, dans quelques années quand même) tu feras peut-être l'inverse : chercher une égalité sous forme de point fixe car on a aussi quelques résultats pour ceux là...
Pour ta culture et piquer ta curiosité : quand tu seras grand, si tu fais un jour des maths (bon d'accord, dans quelques années quand même) tu feras peut-être l'inverse : chercher une égalité sous forme de point fixe car on a aussi quelques résultats pour ceux là...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
