Moyennes harmonique et arithmétique

[GavrocheC]

Bonjour,
Je me retrouve en difficulté face à la question suivante :

On considère deux réels a et b tels que 0<a<b, et les deux suites (Un) et (Vn), définies par U0=a , V0=b,
Vn+1 la moyenne arithmétique de Un et Vn et Un+1 la moyenne harmonique de Un et Vn.

Montrer que pour tout entier naturel n, Un < Vn

Je pense que la solution ne doit pas être si difficile mais je ne fais que de tourner autour...

Merci d'avance !

[LB2]

Hello!

Soient a et b deux réels positifs
Quelle est l'égalité mathématique que tu peux écrire pour :

- la moyenne arithmétique de a et b ?
- la moyenne harmonique de a et b ?
- (et tant qu'on y est ) la moyenne géométrique de a et b ?

[GavrocheC]

On a M= (a+b)/2
Mh= 2 / (1/a + 1/b) soit 2ab/(a+b)
et Mg = sqrt{a*b} il me semble.

J'ai donc essayé la différence M-Mh et le quotient M/Mh pour montrer que la moyenne est toujours supérieur à la moyenne harmonique. Cependant j'obtiens toujours un résultat qui ne fonctionne pas.

A partir de votre message je me dis que la solution serait peut-être de montrer que Mh<Mg<M ?

(P.S : Désolé pour l'écriture des formules, je vais me pencher sur l'utilisation des balises TEX rapidement)

[mathelot]

bonjour,
moyenne arithmétique m:

moyenne harmonique h: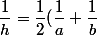

calcule h.

[GavrocheC]

Je viens de trouver !
Merci beaucoup de vos réponse !