Montrer que cette fonction est croissante par dérivation

[ImJenkins]

Bonjour,

Je dois prouver que cette fonction est croissante sur [0, +Infini[ par dérivation mais je ne comprends pas comment faire !

f(x) = 5 - 4/(x+2)

Merci de votre aide !

[capitaine nuggets]

Salut !

Il s'agit simplement d'appliquer des formules de dérivées vues en cours.

[ImJenkins]

Je trouve que la dérivée fait :

F(x) = 5 - 4/(x+2)
Donc
F'(x) = 0 - ( - 4/(x+2)^2)
F'(x) = 4/(x+2)^2

C'est ça?

Si oui, cela est forcément positif... Mais ça me paraît trop simple ?
merci !

[laetidom]

Je trouve que la dérivée fait :

F(x) = 5 - 4/(x+2)
Donc
F'(x) = 0 - ( - 4/(x+2)^2)
F'(x) = 4/(x+2)^2

C'est ça?

Si oui, cela est forcément positif... Mais ça me paraît trop simple ?
merci !

Bonsoir,
Je trouve pareil !

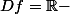
la dérivée étant toujours positive (attention non définie en x= 2 car {}) et comme la dérivée est la pente de la tangente à la courbe, la fonction est donc croissante !