Démontrer que cette suite est croissante.

par **jeep22** » 27 Mai 2010, 17:53

Bonjour voila tout est dans le titre. la suite est la suivante :

[CENTER]u1+u2+...+un[/CENTER]
Vn= [CENTER]-------------------[/CENTER]
[CENTER] n[/CENTER]

(Je n'arrive pas du tout)

par **Finrod** » 27 Mai 2010, 18:11

Il faut que

soit positive ^^

par **jeep22** » 27 Mai 2010, 18:27

C'est à dire je ne voit pas du tout comment faire ?

par **Finrod** » 27 Mai 2010, 18:39

OK. J'avais raté un truc.

Pour faire une fraction, utilise les balise [T E X] [ /T E X] et mets y :

\frac{u_{1}+...+u_{n}}{n}

ça donne

voilà. (javais raté le 1/n)

donc là, maintenant, si je me souviens de l'exo, j'essaie de t'aider. (j'ai l'air malin tiens)

par **jeep22** » 27 Mai 2010, 18:43

Finrod a écrit:OK. J'avais raté un truc.

Pour faire une fraction, utilise les balise [T E X] [ /T E X] et mets y :

\frac{u_{1}+...+u_{n}}{n}

ça donne

voilà. (javais raté le 1/n)

donc là, maintenant, si je me souviens de l'exo, j'essaie de t'aider. (j'ai l'air malin tiens)

Merci beaucoup de m'aider à utiliser le site car je suis nouveau.

par **Finrod** » 27 Mai 2010, 18:48

Si

est croissante, alors

or on peut vérifier

donc dans ce cas

est bien croissante.

par **jeep22** » 27 Mai 2010, 18:53

Finrod a écrit:Si est croissante, alors

or on peut vérifier

donc dans ce cas est bien croissante.

Merci, alor la il va faloir que je m'y mette pour comprendre le résonnement ^^

par **Finrod** » 27 Mai 2010, 19:13

Raisonnement avec "ai". avec é, c'est pour les cloches.

Si

est croissante alors chaque

est majoré par

donc

est majoré par la somme de n fois le terme

(qui vaut n *

), le tout sur n. ce qui à l'arrivé fait

.

Ensuite la formule que je donne vient du fait que

est juste la somme des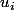

donc

Après tu l'écris différemment en divisant par n+1 et par

.

Donc à gauche, il te reste le rapport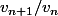

Et à droite comme

, le terme du haut est plus grand que n+1, soit que le terme du bas.

Donc

est croissante.

par **jeep22** » 27 Mai 2010, 19:26

correction de l'énnoncé: Il faut montrer que Vn est positive et on sais que Un est croissante.

par **Finrod** » 28 Mai 2010, 13:31

C'est faux.

Il manque encore des hypothèses. Il faudrait que

ait une limite positive ou soit non bornée.

par **azziz** » 28 Mai 2010, 19:33

bonsoir
peut etre il y a une manque de donnees et si Un=(-1)^n ?

par **Finrod** » 28 Mai 2010, 19:37

azziz a écrit:bonsoir
peut etre il y a une manque de donnees et si Un=(-1)^n ?

Il a dit qu'elle était croissante...

Démontrer que cette suite est croissante.

démontrer que cette suite est croissante.

Qui est en ligne