f (x) = x−2+1 ln x
Montrer que l'équation f (x)=0 admet dans ]0;+∞[ une solution unique s. Donner une valeur
approchée de s à 10−2 près.
Je tente de résoudre cette équation mais n'y parvient pas. Quelqu'un peut il m'aider stp?
Montrer que f(x)=0 admet une équation unique
9 messages
- Page 1 sur 1
Re: montrer que f(x)=0 admet une équation unique
Bonjour;
tu ne pourras pas résoudre directement cette équation, mais au contraire tu pourras faire une étude de la fonction définie pour tout
définie pour tout 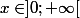 par
par  = x-2+ln(x)) .
.
1) On a : .
.
2) est continue et dérivable sur
est continue et dérivable sur  comme somme de fonctions dérivables sur
comme somme de fonctions dérivables sur  .
.
3)=1+\dfrac{1}{x}) .
.
>0) ; donc
; donc  est strictement croissante sur
est strictement croissante sur  .
.
On a : = - 1) et
et  = ln(2)) ; donc
; donc  f(2) < 0) ; donc en appliquant le théorème des valeurs intermédiaires l'équation
; donc en appliquant le théorème des valeurs intermédiaires l'équation  = 0) admet au moins une solution : soit
admet au moins une solution : soit  cette solution .
cette solution .
Comme est strictement croissante , alors
est strictement croissante , alors  est unique .
est unique .
Je te laisse donner une valeur approchée de à
à 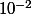 près.
près.
tu ne pourras pas résoudre directement cette équation, mais au contraire tu pourras faire une étude de la fonction
1) On a :
2)
3)
On a :
Comme
Je te laisse donner une valeur approchée de
Re: montrer que f(x)=0 admet une équation unique
Merci pour votre réponse.
Je me rends compte que j'ai fait une erreur dans l'énoncé.
la fonction est la suivante: f (x) = x−2+ 1/2 ln x
J'ai donc f'(x)= 1+1/2x
f'>0 sur Df. La fonction est continue et croissante sur Df également donc il y a bien une solution s unique d'après le théorème des valeurs intermédiaires mais je n'arrive pas à la calculer
f(1)=-1 et f(2)=1/2 ln2 donc 1<s<2 mais c'est un encadrement et pas une une valeur
approchée de s à 10−2 près.
Je me rends compte que j'ai fait une erreur dans l'énoncé.
la fonction est la suivante: f (x) = x−2+ 1/2 ln x
J'ai donc f'(x)= 1+1/2x
f'>0 sur Df. La fonction est continue et croissante sur Df également donc il y a bien une solution s unique d'après le théorème des valeurs intermédiaires mais je n'arrive pas à la calculer

f(1)=-1 et f(2)=1/2 ln2 donc 1<s<2 mais c'est un encadrement et pas une une valeur
approchée de s à 10−2 près.
Re: montrer que f(x)=0 admet une équation unique
poyvroud a écrit:Merci pour votre réponse.
Je me rends compte que j'ai fait une erreur dans l'énoncé.
la fonction est la suivante: f (x) = x−2+ 1/2 ln x
J'ai donc f'(x)= 1+1/2x
f'>0 sur Df. La fonction est continue et croissante sur Df également donc il y a bien une solution s unique d'après le théorème des valeurs intermédiaires mais je n'arrive pas à la calculer
f(1)=-1 et f(2)=1/2 ln2 donc 1<s<2 mais c'est un encadrement et pas une une valeur
approchée de s à 10−2 près.
tu emploies la même notation pour une muliplication et pour une division
il faut écrire 1/(2x) pour la dérivée
Re: montrer que f(x)=0 admet une équation unique
Alors je recommence avec la bonne notation:
f (x) = x−2+ (1/2) ln x
etf'(x)= 1+1/(2x)
Du coup quelqu'un peut il m'aider à résoudre mon problème?
f (x) = x−2+ (1/2) ln x
etf'(x)= 1+1/(2x)
Du coup quelqu'un peut il m'aider à résoudre mon problème?
Re: montrer que f(x)=0 admet une équation unique
tu as ,au moins, trois algorithmes différents pour déterminer des valeurs approchées de la racine:
- le balayage de l'intervalle ]1;2[
- la recherche par dichotomie
(en grec, dichotomie veut dire couper en deux)
- la méthode de Newton
voici un algorithme de balayage (calculatrice TI):
1 STO x
10^{-1} STO h
0 STO y
WHILE x-2-0.5 ln(x) < 0
x STO y
x+h STO x
ENDWHILE
DISP "la racine est comprise entre les valeurs ",y,x
à faire tourner une fois.
A faire tourner une seconde fois en initialisant x avec y
et
remarque x STO y signifie que l'on sauvegarde la valeur de x dans la zone mémoire y
- le balayage de l'intervalle ]1;2[
- la recherche par dichotomie
(en grec, dichotomie veut dire couper en deux)
- la méthode de Newton
voici un algorithme de balayage (calculatrice TI):
1 STO x
10^{-1} STO h
0 STO y
WHILE x-2-0.5 ln(x) < 0
x STO y
x+h STO x
ENDWHILE
DISP "la racine est comprise entre les valeurs ",y,x
à faire tourner une fois.
A faire tourner une seconde fois en initialisant x avec y
et
remarque x STO y signifie que l'on sauvegarde la valeur de x dans la zone mémoire y
Re: montrer que f(x)=0 admet une équation unique
Y a t il une solution autre qu'un programme de calculatrice pour trouver la solution? Je ne sais pas si une justification de ce type est acceptée à l'écrit.
Re: montrer que f(x)=0 admet une équation unique
Il est recommandé de faire une recherche par dichotomie.
tu sais que f(1) <0 < f(2) donc 1 < s < 2 (intervalle de longeur 1)
tu calcules f(1.5) et tu déduis que s est dans un intervalle de longeur (1/2)
tu calcules f(milieu de l'intervalle) et en déduis que s est dans un intervalle de longeur (1/4) ...
au bout de quelques itérations tu auras
f(x1) < 0 < f(x2) donc x1 < s < x2 avec x2 - x1 < 0.01.
tu sais que f(1) <0 < f(2) donc 1 < s < 2 (intervalle de longeur 1)
tu calcules f(1.5) et tu déduis que s est dans un intervalle de longeur (1/2)
tu calcules f(milieu de l'intervalle) et en déduis que s est dans un intervalle de longeur (1/4) ...
au bout de quelques itérations tu auras
f(x1) < 0 < f(x2) donc x1 < s < x2 avec x2 - x1 < 0.01.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: montrer que f(x)=0 admet une équation unique
Salut,
Pour trouver une valeur approchée de la solution de l'équation f(x) = 0, tu peux tracer la fonction avec la calculatrice et regarder l'abscisse du point d'intersection de Cf et et de l'axe des abscisses.
Puis une fois cette valeur approximative trouvée, tu affiches le tableau des valeurs qui démarre à celle-ci. Et tu règles le pas à 0,005.
Dès que tu trouves deux valeurs dont l'une a une image positive et l'autre négative tu peux en déduire une valeur approchée à 0,01 près de la solution.
Pour trouver une valeur approchée de la solution de l'équation f(x) = 0, tu peux tracer la fonction avec la calculatrice et regarder l'abscisse du point d'intersection de Cf et et de l'axe des abscisses.
Puis une fois cette valeur approximative trouvée, tu affiches le tableau des valeurs qui démarre à celle-ci. Et tu règles le pas à 0,005.
Dès que tu trouves deux valeurs dont l'une a une image positive et l'autre négative tu peux en déduire une valeur approchée à 0,01 près de la solution.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
