Montrer qu'un point appartient à un plan

[LéaM1213]

Bonsoir, je n'arrive pas à trouver la réponse d'une question
Donc voila à quoi ressemble mon exercice:
Soit A(−1;0 ;1) , B(1; 4 ;−1) , C(3;−4 ;−3) et S(4 ;0;4) quatre points de l’espace.
1. Démontrer que le triangle ABC est un triangle rectangle en A.
C'est fait
2. a) Démontrer que le vecteur ⃗SO est orthogonal aux deux vecteurs ⃗AB et ⃗AC .
C'est fait
b) En déduire une équation du plan (ABC)
Donc c'est x+z-2=0
Les coefficients a,b et c sont donnés par les coordonnées du vecteur normal ⃗n et le coefficient
d est donné à l’aide d’un des points du plan P
c) Vérifier que le point O appartient au plan (ABC)

Voila pouvez vous m'aider s'ils vous plaît.

J'ai fait les questions et la je suis bloqué à la c). Je ne sais pas quoi faire.

[LéaM1213]

Bien-sûr j'ai remarqué que on est sur un repère (o;i;j;k) donc O=(0;0;0) c'est cela?

[azf]

2. a) Démontrer que le vecteur ⃗SO est orthogonal aux deux vecteurs ⃗AB et ⃗AC .

Bonjour

Je sais bien que vous l'avez fait mais moi je suis obligé de le faire pour passer à la question que vous n'avez pas fait et pour laquelle vous demandez de l'aide

Sauf que je n'arrive pas à lire ceci
Démontrer que le vecteur ⃗SO est orthogonal aux deux vecteurs ⃗AB et ⃗AC .

c'est quoi ⃗SO???? ⃗AB ???? ⃗AC ????

De plus ok je vois un point O dans le ⃗SO mais on ne dit rien sur lui
mais comment parler de lui si on ne le connait pas?

[Vassillia]

Bonsoir,
Le point O est l'origine du repère, il a bien pour coordonnées (0;0;0)

[azf]

oui je n'avais pas vu votre second post c'est O de l'origine
sinon pour les carctères spéciaux que vous avez placés je n'arrive pas à les lire

[LéaM1213]

Oui excusez moi, donc c'est démontrer que SO est orthogonal aux vecteur AB et AC.
A(−1;0 ;1) , B(1; 4 ;−1) , C(3;−4 ;−3) et S(4 ;0;4
AB=(2;4;-2) et AC=(4;-4;-4)
Les deux vecteurs sont orthogonaux: 2x4+4x(-4)+(-2)x(-4)=0
SO=(4;0;4)
J'ai fait AB.SO=2x4+4x0-2x4=0
AC.SO=4x4-4x0-4x4=0
Donc pareil.

Ensuite j'ai trouvé l'équation du plan avec le système:
2a+4b-2c=0
4a-4b-4c=0
Donc x+z-2=0 et n(1;0;1)

Voila et donc je suis bloqué à : Vérifier que le point O appartient au plan (ABC).

[Vassillia]

Il y a un souci dans l'équation du plan
On veut l'équation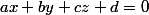 et on utilise un vecteur normal calculé précédemment pour en déduire a, b et c. Un vecteur normal est orthogonal à tous les vecteurs directeurs du plan, on peut prendre lequel ?
Ensuite seulement on remplace par les coordonnées d'un point pour trouver d

PS : ton vecteur SO comporte des erreurs de signe

[annick]

Bonjour,
si ton équation de plan est bien x+z-2=0, alors O(0,0,0), ne peut appartenir à ce plan car ses coordonnées ne vérifient pas l'équation du plan.

[LéaM1213]

J'ai vraiment du mal.
Donc voila ce que j'ai fait:
2a+4b-2c=0
4a-4b-4c=0

Le système donne a=c et donc b=0, on peut choisir a=1 d'où c=1
l'équation du plan donne x+0y+z+d=0, soit x+z-2=0.
Cela nous donne pas un vecteur normal n(1;0;1)?

Et je ne trouve pas mon erreur de signe pour SO

[Vassillia]

D'accord pour a=1; b=0 ; et c=1 mais comment tu trouves d ?
Disons que tu as donné le vecteur OS au lieu du vecteur SO, je pense que cela devrait t'aider à comprendre le problème

[LéaM1213]

Ah d'accord donc pour SO c'est (-4;0;4) merci!
Ensuite pour d j'ai x+0y+z+d=0, donc 1+0+1=2 et 1+0+1-2=0 alors d=2
soit x+z-2=0.

[azf]

Bonjour,
si ton équation de plan est bien x+z-2=0, alors O(0,0,0), ne peut appartenir à ce plan car ses coordonnées ne vérifient pas l'équation du plan.

Justement elle s'est trompée

[Vassillia]

Euh pour SO, le signe pour la dernière coordonnée est aussi -

Mais revenons à l'objectif principal, tu mélanges un peu tout, ax+by+cz+d=0 c'est l'équation du plan, tu viens d'apprendre que a=1; b=0 et c=1 donc tu trouves 1x+0y+1z+d=0
Comment trouver d ? Il faut remplacer x, y et z par les coordonnées d'un point qui appartient au plan

[LéaM1213]

Donc par exemple avec les coordonnées de A(-1;0;1), ce qui nous donne:
1x-1+0x0+1x1=2 et donc d est bien égal à 2?

[LéaM1213]

Eu pardon donc la réponse est -2

[Vassillia]

Ok pour prendre le point A mais que vaut ?
Moi je ne trouve pas 2, à mon avis tu n'as pas fait attention au signe

[azf]

pardon mais vous vous êtes trompée en calculant l'équation du plan

b) En déduire une équation du plan (ABC)
Donc c'est x+z-2=0

c'est pas ça

[Vassillia]

Ben, non, ce n'est pas -2 non plus, prends le temps stp pour ne pas tromper

[LéaM1213]

ha non d =0 c'est ça?

[Vassillia]

Oui, tu vas voir que ce sera beaucoup plus facile pour la suite désormais