Montrer qu'un nombre n'appartient pas à N
19 messages
- Page 1 sur 1
 Montrer qu'un nombre n'appartient pas à N
Montrer qu'un nombre n'appartient pas à N
Bonjour j'ai un exercice à faire .Merci de m'aider :
Soient (a;b) €N* et a>b
Montrez que:
(a^2+b^2)/(a^2-b^2) n'appartient pas à N
Merci☺☺
Soient (a;b) €N* et a>b
Montrez que:
(a^2+b^2)/(a^2-b^2) n'appartient pas à N
Merci☺☺
Re: Montrer qu'un nombre n'appartient pas à N
Salut,
Je trouve rien d'élémentaire comme méthode à part un truc qui va te sembler complètement "sorti d'un chapeau" :
On suppose que est un entier (avec
est un entier (avec  entiers).
entiers).
Bien évidement\!-b) et
et ) sont des entiers (à priori des entiers relatifs).
sont des entiers (à priori des entiers relatifs).
Sauf que si on écrit et
et  uniquement en fonction de
uniquement en fonction de  et
et  , on vérifie facilement que
, on vérifie facilement que  , que
, que  , que
, que  et que
et que  .
.
Et ça, ben c'est une contradiction vu que ça signifie que lorsqu'on a une solution) à l'équation
à l'équation  on peut en trouver une autre "strictement plus petite".
on peut en trouver une autre "strictement plus petite".
Or partant d'un entier naturel , on ne peut pas construire indéfiniment des entiers naturels de plus en plus petit (strictement).
, on ne peut pas construire indéfiniment des entiers naturels de plus en plus petit (strictement).
Je trouve rien d'élémentaire comme méthode à part un truc qui va te sembler complètement "sorti d'un chapeau" :
On suppose que
Bien évidement
Sauf que si on écrit
Et ça, ben c'est une contradiction vu que ça signifie que lorsqu'on a une solution
Or partant d'un entier naturel
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Montrer qu'un nombre n'appartient pas à N
Merci Ben ☺
J'ai pas fait attention à ce truc
l'exercice avait deux questions
La deuxième
M.q ( \/n) / ( \/(n+2)) n'appartient pas à Q
Merci beaucoup
J'ai calculé (A^2+B^2)/(A^2-B^2) et j'ai pas trouvé N
J'ai pas fait attention à ce truc
l'exercice avait deux questions
La deuxième
M.q ( \/n) / ( \/(n+2)) n'appartient pas à Q
Merci beaucoup
J'ai calculé (A^2+B^2)/(A^2-B^2) et j'ai pas trouvé N
Re: Montrer qu'un nombre n'appartient pas à N
peut être passer par = p/q avec p et q premiers entre eux
puis élever au carré
puis élever au carré
Re: Montrer qu'un nombre n'appartient pas à N
Donc
Sinon, au niveau du raisonnement, plutôt que de faire une "descente infinie", c'est sans doute plus simple de dire que vu qu'en multipliant (ou divisant)
Et dans ce cas, la contradiction provient du fait que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Montrer qu'un nombre n'appartient pas à N
Bonjour
@ben314, belle démonstration et particulièrement recherchée. Je me demande d'où vient cette idée de départ?
Par contre j'ai une démonstration plus simpliste. (Bien entendu) a et b étant supposés premier entre eux, il en est de même pour et
et  . Or ceci contredit l'égalité de départ qui est équivalente avec
. Or ceci contredit l'égalité de départ qui est équivalente avec
+b^2(1+N)=0)
@ben314, belle démonstration et particulièrement recherchée. Je me demande d'où vient cette idée de départ?
Par contre j'ai une démonstration plus simpliste. (Bien entendu) a et b étant supposés premier entre eux, il en est de même pour
Re: Montrer qu'un nombre n'appartient pas à N
Salut,
Soient
Soit
Supposons que :

) ou
ou ) multiple de 2,3 et/ou 5
multiple de 2,3 et/ou 5
Soit
J'ai pas eu le temps de finir, mais en gros :
Si \rightarrow q= \sqrt{\alpha} ... \in \R - \Q)
Si \rightarrow q=\frac{1}{\sqrt{\alpha}} ... \in \R - \Q)
Cordialement.
Soient
Soit
Supposons que :
Soit
J'ai pas eu le temps de finir, mais en gros :
Si
Si
Cordialement.
Re: Montrer qu'un nombre n'appartient pas à N
La façon dont j'ai trouvé la "descente" est pas super compliqué : vu la tête de l'énoncé avec un dénominateur que se factorise super gentiment, ça incite un max à poser x=a+b et y=a-b qui donne (calculs)  soit encore
soit encore  .
.
Et là, si on a déjà résolu ce type de problème d'arithmétique qui se résout par "descente infinie" (merci Mr Fermat...) on sait que ce qu'il faut considérer, c'est la solution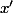 autre que
autre que  de l'équation du second degré
de l'équation du second degré  vu que clairement, le couple (x',y) vérifiera la même équation que le couple (x,y).
vu que clairement, le couple (x',y) vérifiera la même équation que le couple (x,y).
Au niveau calculs, vu les relations coeff. / racines, on a x+x'=2Ny (et xx'=y²) donc x'=2Ny-x et si on veut revenir au problème de départ sans faire référence au changement de variable, il suffit de considérer l'image réciproque du couple (x',y) par la fonction (bijective) (a,b)->(a+b,a-b). Et bien sûr, cet image réciproque, c'est le couple (A,B) du post çi dessus.
Sinon, là :+b^2(1+N)=0) , c'est à dire
, c'est à dire a^2\!=\!(N\!+\!1)b^2) plus le fait que a² et b² sont premiers entre eux, ben tout ce que j'arrive à en déduire c'est que
plus le fait que a² et b² sont premiers entre eux, ben tout ce que j'arrive à en déduire c'est que  et que
et que  (avec
(avec  entier), mais je vois pas bien où réside la contradiction...
entier), mais je vois pas bien où réside la contradiction...
P.S. Et concernant la prose de FLBP, ben je comprend que dalle à ce qu'il écrit.
Le seul truc que je crois comprendre, c'est qu'il veut montrer le résultat en montrant que sqrt((N+1)/(N-1)) n'est jamais un rationnel lorsque N est un naturel>=2, mais vu qu'en fait c'est la deuxième question de l'exercice posé à ayoubjab (c.f. son deuxième post), ben ça m'étonnerais que ce soit ça qui est attendu...
Et là, si on a déjà résolu ce type de problème d'arithmétique qui se résout par "descente infinie" (merci Mr Fermat...) on sait que ce qu'il faut considérer, c'est la solution
Au niveau calculs, vu les relations coeff. / racines, on a x+x'=2Ny (et xx'=y²) donc x'=2Ny-x et si on veut revenir au problème de départ sans faire référence au changement de variable, il suffit de considérer l'image réciproque du couple (x',y) par la fonction (bijective) (a,b)->(a+b,a-b). Et bien sûr, cet image réciproque, c'est le couple (A,B) du post çi dessus.
Sinon, là :
Perso, partant deaviateur a écrit:...a et b étant supposés premier entre eux, il en est de même pouret
. Or ceci contredit l'égalité de départ qui est équivalente avec
P.S. Et concernant la prose de FLBP, ben je comprend que dalle à ce qu'il écrit.
Le seul truc que je crois comprendre, c'est qu'il veut montrer le résultat en montrant que sqrt((N+1)/(N-1)) n'est jamais un rationnel lorsque N est un naturel>=2, mais vu qu'en fait c'est la deuxième question de l'exercice posé à ayoubjab (c.f. son deuxième post), ben ça m'étonnerais que ce soit ça qui est attendu...
Modifié en dernier par Ben314 le 25 Sep 2017, 18:50, modifié 3 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Montrer qu'un nombre n'appartient pas à N
Sinon, j'ai éventuellement une autre méthode plutôt plus simple :
En fait, .
.
Si on écrit que sous forme irréductible, c'est à dire avec
sous forme irréductible, c'est à dire avec \!=\!1) , on a alors
, on a alors ) .
.
Sauf que\!=\!\text{pgcd}(q,p)\!=\!1) donc la fraction
donc la fraction  est elle aussi irréductible et l'égalité (*) entraine l'égalité des numérateurs et celle des dénominateurs.
est elle aussi irréductible et l'égalité (*) entraine l'égalité des numérateurs et celle des dénominateurs.
Ca signifie qu'on a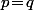 c'est à dire que
c'est à dire que  c'est à dire que
c'est à dire que 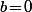 .
.
En fait,
Si on écrit que
Sauf que
Ca signifie qu'on a
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Montrer qu'un nombre n'appartient pas à N
aviateur a écrit:Bonjour
@ben314, belle démonstration et particulièrement recherchée. Je me demande d'où vient cette idée de départ?
Je suis d'accord. Très élégante@
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Montrer qu'un nombre n'appartient pas à N
Rebonjour
En effet cela manque de détails, je suis allé un peu vite:
a^2(1-n)+b^2(1+n)=0 n'est pas possible car a et b ne pouvant être pairs tous les deux il se passent les choses suivantes:
si a et b sont impairs c'est impossible car modulo 4 on a 0=a^2(1-n)+b^2(1+n) =(1-n)+(1+n)=2 (imp).
donc l'un est pair et l'autre impair mais encore impossible en regardant l'exposant de 2.
Par exemple si a est pair , n+1 et n-1 sont pairs. Soit x l'exposant de 2 dans n-1 celui de 2 dans n+1 et 1.
Donc l'exposant de a^2(1-n) est au moins x+2 alors que celui de b^2(1+n) est seulement 1.
Idem si b est pair.
Perso, partant de , c'est à dire plus le fait que a² et b² sont premiers entre eux, ben tout ce que j'arrive à en déduire c'est que et que (avec entier), mais je vois pas bien où réside la contradiction...
En effet cela manque de détails, je suis allé un peu vite:
a^2(1-n)+b^2(1+n)=0 n'est pas possible car a et b ne pouvant être pairs tous les deux il se passent les choses suivantes:
si a et b sont impairs c'est impossible car modulo 4 on a 0=a^2(1-n)+b^2(1+n) =(1-n)+(1+n)=2 (imp).
donc l'un est pair et l'autre impair mais encore impossible en regardant l'exposant de 2.
Par exemple si a est pair , n+1 et n-1 sont pairs. Soit x l'exposant de 2 dans n-1 celui de 2 dans n+1 et 1.
Donc l'exposant de a^2(1-n) est au moins x+2 alors que celui de b^2(1+n) est seulement 1.
Idem si b est pair.
Re: Montrer qu'un nombre n'appartient pas à N
Je comprend toujours pas bien : si b est impair et que l'exposant de 2 dans a est E (>=1) alors de (n-1)a^2=(n+1)b^2 tout ce que je déduit, c'est que 2^(2E) divise n+1 donc 4 divise n+1 et ça prouve que l'exposant de 2 dans n-1 est 1 mais je vois toujours pas de contradiction...aviateur a écrit:Par exemple si a est pair , n+1 et n-1 sont pairs. Soit x l'exposant de 2 dans n-1 celui de 2 dans n+1 et 1. <= ??????
Donc l'exposant de a^2(1-n) est au moins x+2 alors que celui de b^2(1+n) est seulement 1.
Idem si b est pair.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Montrer qu'un nombre n'appartient pas à N
Bonjour
(n-1)a^2=(n+1)b^2.
Le membre de gauche est pair et b^2 étant impair il vient que n+1 est pair. Il en est donc de même pour n-1.
n-1 étant exclus soit x(>=1) l'exposant de 2 dans n-1 et E l'exposant de A. L'exposant de 2 dans (n-1)a^2 est 2E+x>=3.
L'exposant de 2 dans n+1 est 1 si x>1. (n-1=2^x*c, donc n+1=2^x c+2=2(2^(x-1) c+1))
donc a gauche l'exposant est au moins 3 et à droite 1. C'est pas possible.
Donc si x=1; n-1=2 d (avec d impair) n+1=2d+2=2(d+1)
en divisant par 2 l'égalité on a :
a^2 d=b^2(d+1) ou encore d(a^2-b^2)=b^2. mais comme b^2 est premier avec a^2-b^2, b^2 divise d
donc d=z b^2 (z entier)
il vient z(a^2-b^2)=1=z(a-b)(a+b) là ce n'est pas possible non plus. ça marche?
Je suis désolé mais je vais travailler ... En tout cas merci @ben de relever mes imprécisions.
Je pense que le cas symétrique devrait marcher.
De toute façon je reste d'accord avec ta démo mais c'est toujours utile d'en voir d'autres.
(n-1)a^2=(n+1)b^2.
Le membre de gauche est pair et b^2 étant impair il vient que n+1 est pair. Il en est donc de même pour n-1.
n-1 étant exclus soit x(>=1) l'exposant de 2 dans n-1 et E l'exposant de A. L'exposant de 2 dans (n-1)a^2 est 2E+x>=3.
L'exposant de 2 dans n+1 est 1 si x>1. (n-1=2^x*c, donc n+1=2^x c+2=2(2^(x-1) c+1))
donc a gauche l'exposant est au moins 3 et à droite 1. C'est pas possible.
Donc si x=1; n-1=2 d (avec d impair) n+1=2d+2=2(d+1)
en divisant par 2 l'égalité on a :
a^2 d=b^2(d+1) ou encore d(a^2-b^2)=b^2. mais comme b^2 est premier avec a^2-b^2, b^2 divise d
donc d=z b^2 (z entier)
il vient z(a^2-b^2)=1=z(a-b)(a+b) là ce n'est pas possible non plus. ça marche?
Je suis désolé mais je vais travailler ... En tout cas merci @ben de relever mes imprécisions.
Je pense que le cas symétrique devrait marcher.
De toute façon je reste d'accord avec ta démo mais c'est toujours utile d'en voir d'autres.
Re: Montrer qu'un nombre n'appartient pas à N
Bonjour,
Bonjour,
On peut supposer a et b premiers entre eux, car sinon...on les divise par leur pgcd, bref déjà dit.
|(a^2+b^2) \Rightarrow (a+b)|(a^2+b^2) \Rightarrow (a+b)|2ab) .
.
a et b premiers entre eux, donc a+b premier avec a et avec b, donc (a+b) divise 2, donc a+b= 1 ou 2. Impossible avec l'énoncé.
Bonjour,
On peut supposer a et b premiers entre eux, car sinon...on les divise par leur pgcd, bref déjà dit.
a et b premiers entre eux, donc a+b premier avec a et avec b, donc (a+b) divise 2, donc a+b= 1 ou 2. Impossible avec l'énoncé.
Re: Montrer qu'un nombre n'appartient pas à N
Bonjour,
Pour la question 2
Si on pose m=n+1 , on a rac(n)/rac(n+2)=rac(m-1)/rac(m+1)
Supposons que ce nombre soit élément de Q, il s'écrit alors p/q
on a rac(m-1)/rac(m+1) = p/q avec p et q dans N, avec p <q car m-1<m+1.
On élève au carré, (m-1)/(m+1)=p²/q²
ou mq²-q²=mp²+p²
ou m(q²-p²)=q²+p²
ou m=(q²+p²)/(q²-p²)
or m est entier ce qui est impossible d'après la question 1.
Pour la question 2
Si on pose m=n+1 , on a rac(n)/rac(n+2)=rac(m-1)/rac(m+1)
Supposons que ce nombre soit élément de Q, il s'écrit alors p/q
on a rac(m-1)/rac(m+1) = p/q avec p et q dans N, avec p <q car m-1<m+1.
On élève au carré, (m-1)/(m+1)=p²/q²
ou mq²-q²=mp²+p²
ou m(q²-p²)=q²+p²
ou m=(q²+p²)/(q²-p²)
or m est entier ce qui est impossible d'après la question 1.
Re: Montrer qu'un nombre n'appartient pas à N
Rebonjour
Oui@pseuda cela me semble correct mais alors pourquoi on ne l'a pas vu ?
Oui@pseuda cela me semble correct mais alors pourquoi on ne l'a pas vu ?
Re: Montrer qu'un nombre n'appartient pas à N
Bonsoir aviateur,
Oui merci, bizarre, cette démo est pourtant simple.
Oui merci, bizarre, cette démo est pourtant simple.
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
