Matrices
16 messages
- Page 1 sur 1
Re: Matrices
Rebonjour
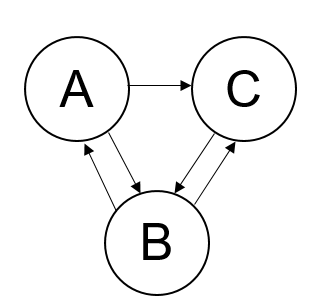
Pour alléger un peu, je noterai A_n, B_n, C_n les événements "être sur A àprès n clics" et même chose pour B_n,C_n.
Autrement dit, A_n = (X_n = A) ETC
Puis classiquement, on note a_n = p(A_n) = p(X_n = A) et même chose avec b_n,c_n de sorte que P_n soit la matrice ligne (a_n,b_n,c_n)
Si tu fais un arbre liant A_n B_n,C_n à A_(n+1),B_(n+1),C_(n+1) c'est facile.
Tu commences par trois branches
A_n
B_n
C_n
De probas a_n,b_n,c_n
Puis par exemple, quand on est sur A_n, on peut aller en A_{n+1},B_{n+1},C_{n+1) avec proba 1/2 a chaque fois vu le caractère equiprobable dans les hypothèses.
Meme chose en partant de B_n et C_n.
Du coup, l'arbre est fait.
Avec la.formule des probas totales, on peut alors exprimer a_{n+1}, b_{n+1} et c_{n+1} et les relations obtenues peuvent être écrites matriciellement.
Pour alléger un peu, je noterai A_n, B_n, C_n les événements "être sur A àprès n clics" et même chose pour B_n,C_n.
Autrement dit, A_n = (X_n = A) ETC
Puis classiquement, on note a_n = p(A_n) = p(X_n = A) et même chose avec b_n,c_n de sorte que P_n soit la matrice ligne (a_n,b_n,c_n)
Si tu fais un arbre liant A_n B_n,C_n à A_(n+1),B_(n+1),C_(n+1) c'est facile.
Tu commences par trois branches
A_n
B_n
C_n
De probas a_n,b_n,c_n
Puis par exemple, quand on est sur A_n, on peut aller en A_{n+1},B_{n+1},C_{n+1) avec proba 1/2 a chaque fois vu le caractère equiprobable dans les hypothèses.
Meme chose en partant de B_n et C_n.
Du coup, l'arbre est fait.
Avec la.formule des probas totales, on peut alors exprimer a_{n+1}, b_{n+1} et c_{n+1} et les relations obtenues peuvent être écrites matriciellement.
Pseudo modifié : anciennement Trident2.
Re: Matrices
"Puis par exemple, quand on est sur  , on peut aller en
, on peut aller en ) "
"
Quand on est en A on peut aller soit en B soit en C mais pas en A donc ?
Quand on est en A on peut aller soit en B soit en C mais pas en A donc ?
Modifié en dernier par Krayz le 25 Avr 2018, 18:51, modifié 1 fois.
Bien à vous,
Krayz.
Krayz.
Re: Matrices
En effet, tu as raison.
Ce n'est pas très clair dans l'énoncé mais ça l'est dans le graphe que tu postes dans ton message 2.
Du coup, l'arbre est facile non?
Ce n'est pas très clair dans l'énoncé mais ça l'est dans le graphe que tu postes dans ton message 2.
Du coup, l'arbre est facile non?
Pseudo modifié : anciennement Trident2.
Re: Matrices
Arbre effectué !
Modifié en dernier par Krayz le 25 Avr 2018, 18:51, modifié 1 fois.
Bien à vous,
Krayz.
Krayz.
Re: Matrices
Krayz a écrit:
Voilà, du coup
(a_(n+1), b_(n+1), c_(n+1)) = (a_n, b_n, c_n) M avec
M =
0 ; 0,5 ; 0,5
0,5 ; 0; 0,5
0 ; 1; 0
Pseudo modifié : anciennement Trident2.
Re: Matrices
En déduire une relation entre  ,
,  et
et 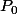 .
.
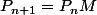
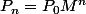
Modifié en dernier par Krayz le 25 Avr 2018, 18:51, modifié 2 fois.
Bien à vous,
Krayz.
Krayz.
Re: Matrices
Krayz a écrit:Oui, voilà
En déduire une relation entre,
et
.
Oui mais c'est plutôt P_n = P_0 M^n.
Pseudo modifié : anciennement Trident2.
Re: Matrices
Bonsoir,
Fait.
Je fais le produit matriciel à la main ou je fais une récurrence ?
2) a) Soit.
Calculeret montrer que
où
et
.
Fait.
2) b) Montrer que pour touton a
Je fais le produit matriciel à la main ou je fais une récurrence ?
Bien à vous,
Krayz.
Krayz.
Re: Matrices
Krayz a écrit:2) b) Montrer que pour touton a
Je fais le produit matriciel à la main ou je fais une récurrence ?
La recurrence semble à portée de main.
Sinon un raisonnement direct marcherait aussi, vu que
Les multiples ne doivent pas être utilisés sans nécessité
Re: Matrices
Il vaut mieux faire un raisonnement direct en faisant le produit à la main, c'est ce qui sera attendu.
Pseudo modifié : anciennement Trident2.
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 163 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :