le propriétaire d'un cinéma de 1 000 places estime , pour ses calculs , qu'il vend 300 billets à 7€ par séance . il a constaté qu'à chaque fois qu'il diminue le prix du billet de 0,1€ , il vend 10 billet de plus . il engage une campagne de promotion .
1- il décide de vendre le billet 5€
a- combien y aura-t-il de spectateurs pour une séance ?
b-quelle est alors la recette pour une séance ?
2-à quelle prix devrait-il vendre le billet pour remplir la salle ? quelle est votre commentaire ?
3-le propriétaire envisage de proposer x réductions de 0,1€
a-quel est alors le prix d'un billet en fonction de x ?
b-exprimez en fonction de x la recette , notée R(x) pour une séance et vérifiez que : R(x)= -x²+40x+2100
c-donnez le tableau de variation de la fonction R sur l'intervalle [0;70]
d-déduisez-en la recette maximale , le prix du billet et le nombre de spectateurs à cette séance
Bonjour , je ne comprends rien à ce devoir maison surtout que nous faisons même pas ce chapitre en classe . Est ce quelqu'un pourrait m'aider ? Merci d'avance
Dm maths problèmes 2nd degré
2 messages
- Page 1 sur 1
Re: dm maths problèmes 2nd degré
Bonjour, lorsque le propriétaire diminue le prix de son billet de 7€ à 5€, il le diminue de 2€ i.e 20 fois 0,1€ de sorte qu'il y aura  spectateurs en plus en comparaison avec les résultats du billet à 7€ donc il y aura 500 spectateurs. S'il y a 500 spectateurs à la séance et que le prix du billet est de 5€, le propriétaire a donc gagné
spectateurs en plus en comparaison avec les résultats du billet à 7€ donc il y aura 500 spectateurs. S'il y a 500 spectateurs à la séance et que le prix du billet est de 5€, le propriétaire a donc gagné  €. On sait que lorsque le billet coûte 7€, il y a 300 spectateurs et que le nombre de spectateurs augmente de 10 lorsque le prix augmente de 0.1€. Ainsi, si on augmente le prix de
€. On sait que lorsque le billet coûte 7€, il y a 300 spectateurs et que le nombre de spectateurs augmente de 10 lorsque le prix augmente de 0.1€. Ainsi, si on augmente le prix de  €, alors cela attire
€, alors cela attire 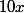 spectateurs par proportionnalité. On note
spectateurs par proportionnalité. On note  le prix du billet et
le prix du billet et  le nombre de spectateurs correspondant, alors
le nombre de spectateurs correspondant, alors ) (au nombre de spectateurs présents lorsque le billet est à 7€, on ajoute le nombre de spectateurs attirés par la différence du prix du billet qui correspond à une différence de
(au nombre de spectateurs présents lorsque le billet est à 7€, on ajoute le nombre de spectateurs attirés par la différence du prix du billet qui correspond à une différence de \times 0,1) €). Or, pour remplir exactement la salle, il faut attirer 1000 spectateurs donc on cherche
€). Or, pour remplir exactement la salle, il faut attirer 1000 spectateurs donc on cherche  tel que
tel que 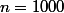 avec les notations précédentes. Ainsi,
avec les notations précédentes. Ainsi, ) puis
puis ) d'où
d'où 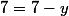 et
et  , cela correspond à un billet gratuit auquel cas la recette est nulle pour le propriétaire : il ne suffit pas de faire baisser le prix du billet (ce qui implique l'augmentation du nombre de spectateurs) pour augmenter la recette, il faut trouver un juste milieu. Le prix du billet sans réduction est 7€ donc le prix du billet après réduction est
, cela correspond à un billet gratuit auquel cas la recette est nulle pour le propriétaire : il ne suffit pas de faire baisser le prix du billet (ce qui implique l'augmentation du nombre de spectateurs) pour augmenter la recette, il faut trouver un juste milieu. Le prix du billet sans réduction est 7€ donc le prix du billet après réduction est  €. D'après le raisonnement effectué précédemment,
€. D'après le raisonnement effectué précédemment, ) en conservant les mêmes notations, en remplaçant y le prix du billet par son expression :
en conservant les mêmes notations, en remplaçant y le prix du billet par son expression :  , on obtient
, on obtient 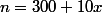 . Le propriétaire gagne
. Le propriétaire gagne  € par spectateur (cela correspond au prix du billet) donc la recette est
€ par spectateur (cela correspond au prix du billet) donc la recette est =(300+10x)(7-0,1x)=-x^2-40x+2100) .
.  est un polynôme du second degré, ton cours te donne ses variations etc..., je te laisse finir. Note bien que j'ai beaucoup rédigé (même trop) pour que tu comprennes, le mieux est que tu écrives toi même ta réponse en essayant de t'affranchir des variables
est un polynôme du second degré, ton cours te donne ses variations etc..., je te laisse finir. Note bien que j'ai beaucoup rédigé (même trop) pour que tu comprennes, le mieux est que tu écrives toi même ta réponse en essayant de t'affranchir des variables  et
et  que j'ai introduites, si t'as bien compris tu devrais y arriver.
que j'ai introduites, si t'as bien compris tu devrais y arriver.
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
