MATHS EXPERTES : Question nombres premiers théorème de Gauss

[ANTHONYP]

Bonjour, soit un entier relatif n tel que : n² = 17p + 1 où p est un nombre premier.
1. Écrire 17p comme un produit de facteurs fonction de n.
2. Montrer que n est de la forme : n = 17k + 1 ou n = 17k-1 avec k un entier relatif. On citera le théorème utilisé.
3. Montrer qu'une seule valeur de k convient.
En déduire les valeurs de n et de p

Voilà je bloque pour la troisième question, pour la 1. j'ai trouvé 17p = (n-1)(n+1) et pour la 2. p = (n-1)(n+1)/17 donc 17 divise (n-1)(n+1) et comme 17 est premier d'après le théorème de Gauss 17 divise n-1 ou 17 divise n+1 soit n = 17k + 1 ou n = 17k - 1. Je n'arrive pas à montrer qu'il y a une seule valeur de k qui convient mais pour autant je sais que k va être égal à 1. Quelqu'un peut m'aider ?

[Ben314]

Salut,
Si tu suppose que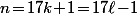 tu en déduit quoi ?

[catamat]

Bonjour
Il suffit de remplacer dans n²=17p+1
A près développement et réduction on en déduit que k divise p et comme p est premier....

[ANTHONYP]

Bonjour
Il suffit de remplacer dans n²=17p+1
A près développement et réduction on en déduit que k divise p et comme p est premier....

Est ce qu'il faut montrer ducoup que k ne peut pas être égal à p aussi ?

[catamat]

Est ce qu'il faut montrer ducoup que k ne peut pas être égal à p aussi ?

C'est pas trop dur quand même...