Mathématiques, tableau de variation

[emelyne14]

Bonjour svp aidez moi je comprends rien merci bcp

Un athlète lance un poid. La hauteur j du poids ( en mètres ) en fonction de la distance x par rapport au lanceur ( en mètres ) est donnée par la fonction suivante :h(x) = -0,07x(au carré ) + 0,84x + 1,96.

1/Établir , le tableau de variation de la fonction h sur l’intervalle [0;14]Justifier
2/a] quelle est la hauteur maximale atteinte par le poids est à quelle distance du lanceur est-elle atteinte ?
B)Calculer la longueur du lancer c’est-à-dire l’endroit où le poids touche le sol .
4/représenter graphiquement avec soin et précision la fonction H sur [0;14]on prendra 1 cm pour 1 m en abscisse et en ordonnée
5/ on cherche à savoir quand le poids est à une altitude strictement supérieur à 4,2 mètres .
A/ montrer que résoudre par calcul le problème revient à résoudre (-0,07x + 0,28 ) ( x-8) > 0.
B/ Résoudre l’inéquation précédent à l’aide d’un tableau de signe sur intervalle un tab résoudre l’inéquation précédent à l’aide d’un tableau de signe sur intervalle [0;14]).
C:comment retrouve-t-on pratiquement ce résultat marqué les traits de lecture sur le graphique d/répondre aux problème

[titine]

Bonjour.

Un athlète lance un poids. La hauteur j du poids ( en mètres ) en fonction de la distance x par rapport au lanceur ( en mètres ) est donnée par la fonction suivante :h(x) = -0,07x(au carré ) + 0,84x + 1,96.

1/Établir , le tableau de variation de la fonction h sur l’intervalle [0;14]Justifier

Relis ton cours sur les fonctions polynômes du second degré. Tu devrais y trouver les indications te permettant de répondre à cette question.
Tu nous dit et on verra après la suite.
Bon courage !

[BenMaths]

Bonjour,

Ici on te propose de décrire une trajectoire avec une fonction en x². En effet les paraboles sont particulièrement bien adaptées pour décrire les trajectoires d'objets lancés à une certaine vitesse et soumis à la gravité.



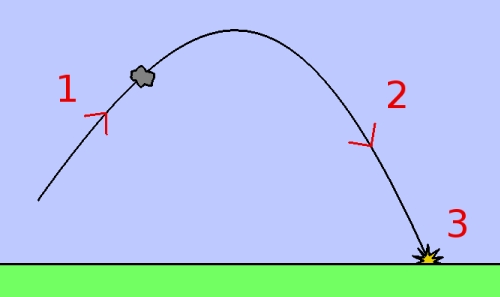
Il faut déjà être au clair sur ce qu'est un tableau de variation, il présente les variation d'une fonction sur un intervalle donné ici [0;14]. Il faut alors te demander de quels outils tu disposes pour étudier les variations d'une fonction polynome de degré 2 : f(x) = - 0.07 x² + 0,84 x + 1,96
Il y a la dérivation, l'allure de la courbe d'une fonction en x², la forme canonique...

[emelyne14]

Merci , donc pour moi pour réaliser le tableau des variations il faut remplacer (x) par un nombre ici de 0 à 14 avec la formule ?

[BenMaths]

Pas exactement.

je te conseil d'aller voir ton cours sur l'étude de la variation des fonctions et sur les polynômes de second degré.

commence par étudier la fonction sur tout son intervalle de définition puis concentre toi sur l'intervalle [0;14]

as-tu vu la dérivation en cours ?

[emelyne14]

COMprends pas

[mathelot]

bonjour,

[titine]

Je suppose que tu as un cours sur les fonctions polynômes du second degré. Tu le lis et on en reparle après.
Ici tu a f( x) = - 0.07 x² + 0,84 x + 1,96 qui est bien de la forme ax² + b x + c
avec a=-0,07 ; b=0,84 et c=1,96