Dm math thales et nombre d'or
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
jean59
- Membre Naturel
- Messages: 17
- Enregistré le: 19 Déc 2008, 10:16
-
 par jean59 » 19 Déc 2008, 12:13
par jean59 » 19 Déc 2008, 12:13
je n'arrive pas les calcul je sais que af/ad=(1+racinede5)/2 sur 1
-
mathelot
 par mathelot » 19 Déc 2008, 12:14
par mathelot » 19 Déc 2008, 12:14
jean59 a écrit:oui c'est bon j'ai trouvé la question 1 mais pas la 2 ni la 3
bah , si. Tu peux connaitre toutes les mesures de longueur
de tous les différents côtés (par Pythagore).
Ensuite, tu écris tes quotients
Où est-ce que ça coince ?
-
jean59
- Membre Naturel
- Messages: 17
- Enregistré le: 19 Déc 2008, 10:16
-
 par jean59 » 19 Déc 2008, 12:15
par jean59 » 19 Déc 2008, 12:15
c'est que je n'arrive pas trop les calcul avec racine
-
mathelot
 par mathelot » 19 Déc 2008, 12:17
par mathelot » 19 Déc 2008, 12:17
est-ce que tu as réussi à démontrer que

Ce nombre s'appelle

. C'est le nombre d'or, le grand
concurrent de

-
jean59
- Membre Naturel
- Messages: 17
- Enregistré le: 19 Déc 2008, 10:16
-
 par jean59 » 19 Déc 2008, 12:18
par jean59 » 19 Déc 2008, 12:18
non je n'ai pas réussi
-
mathelot
 par mathelot » 19 Déc 2008, 12:20
par mathelot » 19 Déc 2008, 12:20
jean59 a écrit:je n'arrive pas les calcul je sais que af/ad=(1+racinede5)/2 sur 1
oui, très bien. AD vaut 1 et AF vaut

, le nombre d'or. :++: :++:
Maintenant, il te faut démontrer que le petit rectangle BFEC
est lui aussi un rectangle d'or, comme le grand AFED.
-
jean59
- Membre Naturel
- Messages: 17
- Enregistré le: 19 Déc 2008, 10:16
-
 par jean59 » 19 Déc 2008, 12:23
par jean59 » 19 Déc 2008, 12:23
mais comment je calcule af/ad? je dois trouver quelle nombre?
-
mathelot
 par mathelot » 19 Déc 2008, 12:25
par mathelot » 19 Déc 2008, 12:25
développe tranquillement le carré de

avec tes identités remarquables:
 ^2 = \frac{A^2}{B^2})
c'est comme ceci que l'on élève un quotient au carré.
Tu écris
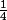
en facteur (le dénominateur)
et tu développes
^2)
avec l'identité remarquable.
Ne stresse pas, ça va aller tout seul.
-
mathelot
 par mathelot » 19 Déc 2008, 12:28
par mathelot » 19 Déc 2008, 12:28
jean59 a écrit:mais comment je calcule af/ad? je dois trouver quelle nombre?
tu l'as trouvé. ton résultat est exact.
c'est
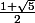
-
jean59
- Membre Naturel
- Messages: 17
- Enregistré le: 19 Déc 2008, 10:16
-
 par jean59 » 19 Déc 2008, 12:29
par jean59 » 19 Déc 2008, 12:29
l'idendité remarquable ca fait 12??
je ne comprends pas trop
et je stresse un peu car je dois avoir fini dans 15min :triste:
-
mathelot
 par mathelot » 19 Déc 2008, 12:32
par mathelot » 19 Déc 2008, 12:32
jean59 a écrit:l'idendité remarquable ca fait 12??
je ne comprends pas trop
et je stresse un peu car je dois avoir fini dans 15min :triste:
bah non,
ca fait

et tu additionne 1+5
-
jean59
- Membre Naturel
- Messages: 17
- Enregistré le: 19 Déc 2008, 10:16
-
 par jean59 » 19 Déc 2008, 12:35
par jean59 » 19 Déc 2008, 12:35
ca fait donc 2racine5+6/4?????
-
mathelot
 par mathelot » 19 Déc 2008, 12:37
par mathelot » 19 Déc 2008, 12:37
vi.
tu simplifie cette somme par 2 et
tu écris ensuite que

-
jean59
- Membre Naturel
- Messages: 17
- Enregistré le: 19 Déc 2008, 10:16
-
 par jean59 » 19 Déc 2008, 12:39
par jean59 » 19 Déc 2008, 12:39
d'accord merci
-
mathelot
 par mathelot » 19 Déc 2008, 12:42
par mathelot » 19 Déc 2008, 12:42
ouf, cette fois, j'y vais.
Pour la dernière question, il suffit de calculer l'inverse du nombre
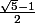
L'inverse de
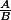
est

tu multiplie par la quantité conjuguée pour retrouver

@++++
-
jean59
- Membre Naturel
- Messages: 17
- Enregistré le: 19 Déc 2008, 10:16
-
 par jean59 » 19 Déc 2008, 12:44
par jean59 » 19 Déc 2008, 12:44
ok merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
