Partage ce devoir avec tes amis !
Sujet du devoir
Bonjour, j'ai un DM de math en trois partie et je sèche sur la troisième depuis plusieurs jours.
Soit la suite (Vn) définie par V0=1, et pour tout entier naturel n: Vn+1=1+(1/Vn)
1)Démontrer que, pour entier naturel n, Vn supérieur ou égale à 1.
2) Vérifier que, pour tout entier naturel n, Vn+1-phi=phi-Vn/Vn x phi.
3) En déduire que, pour tout entier naturel n, l Vn+1-phi l inférieur ou égale 1/phi l Vn-phi l.
4) Démontrer que, pour tout entier naturel n, on a: l Vn-phi l inférieur ou égale (1/phi)^n.
5) En déduire la limite de la suite (Vn).
Où j'en suis dans mon devoir
J'ai réussi à répondre aux deux premières questions sans problèmes mais les inégalités des questions 3 et 4 me posent soucis. J'ai essayé plusieurs techniques comme le raisonnement par récurrence mais je n'arrive jamais à les démontrer.
Je ne demande pas de répondre à ma place mais juste de me dire quelle méthode utilisée pour démontrer ces inégalités.
Merci.
DM de math suite
3 messages
- Page 1 sur 1
Re: DM de math suite
Salut,
Compliqué à lire...
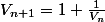
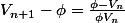
Au fait qu'est (donné dans une question précédente a priori).
(donné dans une question précédente a priori).
Maintenant:
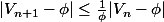 ?
?
Compliqué à lire...
Au fait qu'est
Maintenant:
Re: DM de math suite
Désolé pour la présentation, c'est mon premier post ici.
Phi est le nombre d'or, il correspond à [1+racine de 5/2]
Phi est le nombre d'or, il correspond à [1+racine de 5/2]
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 130 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
