Math exo

[nee-san]

bonjour, j'ai deux exo ou je bloque un peut,

1) A et B sont deux points distincts appartenant à la courbe représentant la fonction définie sur [0; +infini [ par


q1) montrer que le milieu I du segment [AB] est situé en dessous du point J de la courbe ayant le même abscisse?

alors ce que j'ai fait:
soit a et b les abscisse de A et B alors,

alors

et

et pour répondre à la question je me suis dit que j'allais montrer que yi<yj
est ce que je doit faire comme sa et comment le montrer ?

[Dlzlogic]

Bonjour,
Moi, j'étudierais la concavité de la fonction.

[nee-san]

Bonjour,
Moi, j'étudierais la concavité de la fonction.

bonsoir, ca veut dire quoi, ?

et on me dit entre parenthese que si a différent de b alors

donc comment faire avec ce que j'ai si ce que j'ai pour le moment fait est bon?

[nee-san]

aide svp si possible

[nee-san]

up je veut dire

[Pixis]

Ta méthode est très bien il faut montrer que l'une des deux ordonnées est supérieure à l'autre.
Dès qu'il s'agit de comparaison de termes qui comportent des racines, il faut se débrouiller pour "éliminer" ces racines (le plus possible)... Comment faire ? Je te laisse chercher un peu !

[Dlzlogic]

bonsoir, ca veut dire quoi, ?

Ca veut dire que sai la courbe suit le trajet d'un objet que l'on lance en l'ait et qui retombe, le milieu de 2 points A et B sera en dessous de la courbe, si au contraire, c'est un objet que l'on lance par terre et qui va rebondir, le milieu de 2 points A et B sera au-dessus de la courbe.

[nee-san]

Ca veut dire que sai la courbe suit le trajet d'un objet que l'on lance en l'ait et qui retombe, le milieu de 2 points A et B sera en dessous de la courbe, si au contraire, c'est un objet que l'on lance par terre et qui va rebondir, le milieu de 2 points A et B sera au-dessus de la courbe.

mais on n'a jamais vue cela et comment savoir si c'est un objet lancer?

Ta méthode est très bien il faut montrer que l'une des deux ordonnées est supérieure à l'autre.
Dès qu'il s'agit de comparaison de termes qui comportent des racines, il faut se débrouiller pour "éliminer" ces racines (le plus possible)... Comment faire ? Je te laisse chercher un peu !

oki merci, je pense que je doit tout mêtre d'un cotée pour avoir quelquechose>0
et en élevant au carrée voir que c'est positif?

mais comment faire

[Dlzlogic]

Je ne sais pas à quel niveau voue êtes.
Je vois un exercice intéressant, qui admet une solution numérique plus ou moins compliquée à calculer et une solution plus directe.
Mon professeur de math avait l'habitude de dire "il faut être intelligemment paresseux". J'essaye encore de suivre son enseignement.
Question : avez-vous dessiné la courbe représentative de la fonction?

[nee-san]

Je ne sais pas à quel niveau voue êtes.
Je vois un exercice intéressant, qui admet une solution numérique plus ou moins compliquée à calculer et une solution plus directe.
Mon professeur de math avait l'habitude de dire "il faut être intelligemment paresseux". J'essaye encore de suivre son enseignement.
Question : avez-vous dessiné la courbe représentative de la fonction?

oui je les dessiner

niveau 1ere S, les cours qu'on a fait sont second degré et vatiation des fonction de reference
mais je voie pas comment démontrer que yi<yj

[Pixis]

Donc

[Dlzlogic]

Ma méthode de démonstration n'est pas une méthode du type analytique mais synthétique.
1ère piste purement mathématique : étudiez la dérivée seconde.
2ème piste basée sur la logique : f(x) = rac(x) = x^1/2
Etudiez f(x) = x^n
Le plus facile, c'est pour n = 1.
Qu'est ce que ça donne pour n>1 et pour n<1 ?

[Pixis]

Je suis curieux de savoir où mène ton raisonnement avec ton étude de x^n ?

[Anonyme]

@nee-san
Un conseil est de faire un dessin et de dessiner un exemple avec 2 points pour que cela soit plus parlant

Je te conseille donc :
1) de dessiner le graphe de la fonction f
2) de prendre 2 points au hasard sur cette courbe (d'abscisses 2 et 4 par exemple)
3) de dessiner le point I et le point J pour ces 2 points

puis seulement après , tu peux te lancer dans des calculs pour montrer que I est "en dessous" de J
en raisonnant à partir de 2 points quelconques A et B de cette courbe d'abscisses a et b
( avec bien sûr a>=0 et b >=0 )

Ce calcul revient à démontrer que

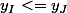
[nee-san]

Donc

merci, je tente un truc mais je suis pas sur:





?

[Pixis]

Oui, développe le résultat de

[nee-san]

Oui, développe le résultat de

oki, alors

?

[Pixis]

Très bien. Tu as donc les deux ordonnées. Comment savoir laquelle est la plus grande ?
Pour montrer que a>b, il suffit de montrer que a-b>0

Adapte ça, et dis moi ce que ça donne

[Dlzlogic]

@ Pixis

Je suis curieux de savoir où mène ton raisonnement avec ton étude de x^n ?

Bon, pour f(x) = 1 la courbe est la première bissectrice. Pas de concavité
Pour n > 1, la courbe est celle de la fonction puissance. f(x) > x concavité tournée vers le haut
Pour n < 1, f(x) < x. concavité tournée vers le bas.
Naturellement dans le domaine de définition concerné.

[Pixis]

Oui, ça je comprends bien, mais pourquoi étudier les 3 cas alors qu'ici nous parlons de la fonction racine, qui à l'évidence est une fonction puissance avec une puissance <1 ?

Ce n'est pas un reproche, j'essaie seulement de comprendre le but de la méthode :)
Peut-être était-ce un rappel général à adapter pour l'exercice ?