Marche aléatoire et conditionnement
20 messages
- Page 1 sur 1
marche aléatoire et conditionnement
Bonsoir,
L’exercice qui va suivre est tiré d’un livre de TS au chapitre « probabilités conditionnelles », et ne fait pas partie des exercices anotés « difficile ».
Problème:
Un robot est posé au centre d’une table carrée de 90 cm de côté.
Toutes les secondes, il effectue un pas de 10cm dans une des quatres directions.
(un schéma suggère de travailler dans un repère orthonormé du plan euclidien ; les directions sont orthogonales aux côtés de la table)
En moyenne, combien de temps le robot reste-t-il sur la table ?
J’ai essayé deux types de résolution, sans toutefois parvenir à une seule solution.
(1) ramener, hélàs non rigoureusement, la situation a un schéma de Bernoulli, puis calculer l’esperance mathématique associée. Ceci s’avère insatisfaisant notamment parce que je n’ai pas de démonstration de la validité du calcul d’une loi binomiale (le cours nous demande de l’admettre), et que je suppose, sans en être convaincu, qu’un temps n tel que le robot ait parcouru neufs pas dans une paire de directions non orthogonales suffit en moyenne pour qu'il tombe de la table.
(2) formaliser que le robot tombe de la table si et seulement si il s’est déplacé au moins 5 fois supplémentaires dans une direction plutôt que la direction opposée, mais je ne suis pas arrivé à résoudre l’équation obtenue.
J’aimerais pouvoir passer plus de temps sur ce problème, mais actuellement je n’en ai pas.
Merci d’avance pour votre aide.
L’exercice qui va suivre est tiré d’un livre de TS au chapitre « probabilités conditionnelles », et ne fait pas partie des exercices anotés « difficile ».
Problème:
Un robot est posé au centre d’une table carrée de 90 cm de côté.
Toutes les secondes, il effectue un pas de 10cm dans une des quatres directions.
(un schéma suggère de travailler dans un repère orthonormé du plan euclidien ; les directions sont orthogonales aux côtés de la table)
En moyenne, combien de temps le robot reste-t-il sur la table ?
J’ai essayé deux types de résolution, sans toutefois parvenir à une seule solution.
(1) ramener, hélàs non rigoureusement, la situation a un schéma de Bernoulli, puis calculer l’esperance mathématique associée. Ceci s’avère insatisfaisant notamment parce que je n’ai pas de démonstration de la validité du calcul d’une loi binomiale (le cours nous demande de l’admettre), et que je suppose, sans en être convaincu, qu’un temps n tel que le robot ait parcouru neufs pas dans une paire de directions non orthogonales suffit en moyenne pour qu'il tombe de la table.
(2) formaliser que le robot tombe de la table si et seulement si il s’est déplacé au moins 5 fois supplémentaires dans une direction plutôt que la direction opposée, mais je ne suis pas arrivé à résoudre l’équation obtenue.
J’aimerais pouvoir passer plus de temps sur ce problème, mais actuellement je n’en ai pas.
Merci d’avance pour votre aide.
Re: marche aléatoire et conditionnement
Salut,
A froid, vu la difficulté mathématique du bidule, j'aurais tendance à penser qu'au niveau Lycée, surtout sans indications supplémentaires, le seul truc faisable, c'est une simulation informatique.
A froid, vu la difficulté mathématique du bidule, j'aurais tendance à penser qu'au niveau Lycée, surtout sans indications supplémentaires, le seul truc faisable, c'est une simulation informatique.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: marche aléatoire et conditionnement
Une simulation avec python me donne une moyenne d'environ 29,2 secondes (avec 1000000 expériences)
Au lycée, ça doit pouvoir se faire avec Algobox
Au lycée, ça doit pouvoir se faire avec Algobox
Re: marche aléatoire et conditionnement
les aspects combinatoires et géométriques du problème m’ayant charmé pendant quelques heures, j’ai omis une phrase de l’énoncé :
« Écrire un algorithme simulant cette expérience »
…
Cela dit, il n’est pas précisé de simuler!
Une savante suggestion concernant le nombre satisfaisant de simulation pour calculer la moyenne ?
« Écrire un algorithme simulant cette expérience »
…
Cela dit, il n’est pas précisé de simuler!
Une savante suggestion concernant le nombre satisfaisant de simulation pour calculer la moyenne ?
Re: marche aléatoire et conditionnement
Si on calcule la valeur exacte, ça donne ça : 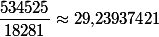 .
.
Mais, même en restant au niveau le plus basique, je sais pas si c'est facile à expliquer au niveau Lycée :
Le plus simple, c'est, pour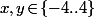 de noter
de noter ) le temps moyen qu'il faut pour que que le robot sorte de la table s'il est en (x,y) au départ puis de dire que :
le temps moyen qu'il faut pour que que le robot sorte de la table s'il est en (x,y) au départ puis de dire que :
\!=\!1\!+\!\frac{1}{4}E(0,1)\!+\!\frac{1}{4}E(1,0)\!+\!\frac{1}{4}E(-1,0)\!+\!\frac{1}{4}E(0,-1))
. . .
\!=\!1\!+\!\frac{1}{4}E(4,2)\!+\!\frac{1}{4}E(3,1)\!+\!\frac{1}{4}E(4,0))
. . .
\!=\!1\!+\!\frac{1}{4}E(4,3)\!+\!\frac{1}{4}E(3,4))
Modulo d'utiliser les symétries\!=\!E(\pm x,\pm y)\!=\!E(\pm y,\pm x)) , ça donne un système de 15 équations à 15 inconnues.
, ça donne un système de 15 équations à 15 inconnues.
Sauf que je sais pas si au niveau Lycée, ce type d'égalité sur des espérances est vu ou pas.
Mais, même en restant au niveau le plus basique, je sais pas si c'est facile à expliquer au niveau Lycée :
Le plus simple, c'est, pour
. . .
. . .
Modulo d'utiliser les symétries
Sauf que je sais pas si au niveau Lycée, ce type d'égalité sur des espérances est vu ou pas.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: marche aléatoire et conditionnement
Merci Ben314 !
Je ne pense pas que ce soit la réponse attendue, mais je la trouve appétissante.
Je ne pense pas que ce soit la réponse attendue, mais je la trouve appétissante.
Re: marche aléatoire et conditionnement
Bonsoir,
c'est une marche aléatoire sur Z^2, on peut modéliser le problème par une chaine de Markov, noter (X_n,Y_n) la position du robot à l'instant n, la matrice de transition est grande mais "relativement simple". Il y a des barrières absorbantes correspondant au bord de la table.
c'est une marche aléatoire sur Z^2, on peut modéliser le problème par une chaine de Markov, noter (X_n,Y_n) la position du robot à l'instant n, la matrice de transition est grande mais "relativement simple". Il y a des barrières absorbantes correspondant au bord de la table.
Re: marche aléatoire et conditionnement
Salut
Est-ce qu'il est possible de calculer la probabilité pour que le robot reste sur la table plus de 5 minutes ?
Est-ce qu'il est possible de calculer la probabilité pour que le robot reste sur la table plus de 5 minutes ?
Re: marche aléatoire et conditionnement
Oui, bien sûr qu'on peut : numériquement parlant, toutes les infos du problème se résument à la matrice de transition concernant les proba. de passage d'une case à une autre à chaque secondes [qui, si on utilise les symétries du problème est une matrice 15x15].
Et calculer exactement la proba que le robot soit encore sur la table au bout de N secondes, ça revient peu ou prou à calculer la matrice en question à la puissance N.
Évidement, mais ça revient au même, on peut chercher l’expression de la proba p_n que le robot soit encore sur la table après n secondes : ça va donner une formule de récurrence d'ordre [au plus] 15 qu'on obtient directement en calculant le polynôme caractéristique [ou minimal] de la matrice en question.
Après, si on veut la forme exacte de p_n en fonction de n exprimé avec "des fonctions élémentaires", ben tout va dépendre du fait que ce polynôme admet ou pas des racines "calculable à l'aide des fonction élémentaires".
Ici, sauf erreur, on peut vu que, selon maple, le polynôme caractéristique se factorise sous la forme
X^2+5/256)(X^4-(5/8)X^2+5/256)(X^4-(5/4)X^2+5/16))
Et calculer exactement la proba que le robot soit encore sur la table au bout de N secondes, ça revient peu ou prou à calculer la matrice en question à la puissance N.
Évidement, mais ça revient au même, on peut chercher l’expression de la proba p_n que le robot soit encore sur la table après n secondes : ça va donner une formule de récurrence d'ordre [au plus] 15 qu'on obtient directement en calculant le polynôme caractéristique [ou minimal] de la matrice en question.
Après, si on veut la forme exacte de p_n en fonction de n exprimé avec "des fonctions élémentaires", ben tout va dépendre du fait que ce polynôme admet ou pas des racines "calculable à l'aide des fonction élémentaires".
Ici, sauf erreur, on peut vu que, selon maple, le polynôme caractéristique se factorise sous la forme
Modifié en dernier par Ben314 le 29 Déc 2018, 12:18, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: marche aléatoire et conditionnement
Oui, je pense que cela est faisable. Le problème sous-jacent essentiel est la marche aléatoire symétrique sur Z (sur un axe) avec barrières absorbantes, plus connu sous le nom de problème de ruine du joueur, dans le cas particulier où la pièce est équilibrée et les deux joueurs ont même capital de départ.
Petit rappel de ce problème :
Le joueur A, possédant initialement a euros, et le joueur B, possédant initialement b euros, décident de miser un euro sur le résultat du lancer d'une pièce, avec les règles suivantes :
- Avec probabilité p, la pièce donne face et le joueur A donne 1 euro au joueur B
- Avec probabilité q=1-p, la pièce donne pile et le joueur A reçoit 1 euro du joueur B.
Ils continuent à lancer la pièce jusqu'à ce que l'un des joueurs soit ruiné (c'est la raison pour laquelle on parle de barrière absorbante). Il existe d'autre versions de ce problème, notamment l'étude d'un joueur à capital fini qui joue contre une banque à capital illimité. On peut également considérer une marche non symétrique (pièce non équilibrée).
Le problème du robot qui se déplace symétriquement avec des pas de 1 sur un axe gradué de -l à +l en partant de l'origine correspond au problème de la ruine du joueur avec p=1/2, a=b=l.
Plus difficile, le problème posé par rdt, du robot qui se déplace symétriquement avec des pas de 1 sur un réseau gradué (table) en partant de l'origine peut s’interpréter comme le problème de la ruine du joueur "à deux dimensions", c'est à dire :
- le joueur A et B jouent avec p=1/2, a=b=l
- Simultanément, le joueur C et D jouent avec p=1/2, c=d=l
- à chaque instant n, on commence par choisir avec probabilité 1/2 si c'est les joueurs A/B ou les joueurs C/D qui vont lancer la pièce, puis on procède comme dans le cas unidimensionnel.
Le jeu s'arrête à la première ruine, la ruine de A correspondant à "le robot atteint le bord haut", la ruine de B à "le robot atteint le bord bas", la ruine de C correspondant à "le robot atteint le bord gauche", la ruine de D correspondant à "le robot atteint le bord droit".
Il existe de multiples façons d'aborder ce problème, on peut avoir une approche "naïve" sans autre outil que l'indépendance et le conditionnement, on peut aussi formaliser avec des chaines de Markov (c'est le genre de calcul que fait Ben avec son E(x,y)), voire avec des processus aléatoires et martingales.
L'approche élémentaire est intéressante mais le détail et l'exposé de toutes ces méthodes dépasse ma compétence, il faut consulter des (bonnes) références sur le sujet.
Petit rappel de ce problème :
Le joueur A, possédant initialement a euros, et le joueur B, possédant initialement b euros, décident de miser un euro sur le résultat du lancer d'une pièce, avec les règles suivantes :
- Avec probabilité p, la pièce donne face et le joueur A donne 1 euro au joueur B
- Avec probabilité q=1-p, la pièce donne pile et le joueur A reçoit 1 euro du joueur B.
Ils continuent à lancer la pièce jusqu'à ce que l'un des joueurs soit ruiné (c'est la raison pour laquelle on parle de barrière absorbante). Il existe d'autre versions de ce problème, notamment l'étude d'un joueur à capital fini qui joue contre une banque à capital illimité. On peut également considérer une marche non symétrique (pièce non équilibrée).
Le problème du robot qui se déplace symétriquement avec des pas de 1 sur un axe gradué de -l à +l en partant de l'origine correspond au problème de la ruine du joueur avec p=1/2, a=b=l.
Plus difficile, le problème posé par rdt, du robot qui se déplace symétriquement avec des pas de 1 sur un réseau gradué (table) en partant de l'origine peut s’interpréter comme le problème de la ruine du joueur "à deux dimensions", c'est à dire :
- le joueur A et B jouent avec p=1/2, a=b=l
- Simultanément, le joueur C et D jouent avec p=1/2, c=d=l
- à chaque instant n, on commence par choisir avec probabilité 1/2 si c'est les joueurs A/B ou les joueurs C/D qui vont lancer la pièce, puis on procède comme dans le cas unidimensionnel.
Le jeu s'arrête à la première ruine, la ruine de A correspondant à "le robot atteint le bord haut", la ruine de B à "le robot atteint le bord bas", la ruine de C correspondant à "le robot atteint le bord gauche", la ruine de D correspondant à "le robot atteint le bord droit".
Il existe de multiples façons d'aborder ce problème, on peut avoir une approche "naïve" sans autre outil que l'indépendance et le conditionnement, on peut aussi formaliser avec des chaines de Markov (c'est le genre de calcul que fait Ben avec son E(x,y)), voire avec des processus aléatoires et martingales.
L'approche élémentaire est intéressante mais le détail et l'exposé de toutes ces méthodes dépasse ma compétence, il faut consulter des (bonnes) références sur le sujet.
Re: marche aléatoire et conditionnement
@Ben : Très bonne idée, je ne connais pas de livre abordant explicitement ces problèmes avec les outils "au programme en prépa"
Sinon, je suis en train de suivre le Mooc sur les probas du MIT, il y a toute une partie sur les chaines de Markov qui termine ce cours, j'en saurais probablement plus sur le sujet d'ici quelques semaines.
Sinon, je suis en train de suivre le Mooc sur les probas du MIT, il y a toute une partie sur les chaines de Markov qui termine ce cours, j'en saurais probablement plus sur le sujet d'ici quelques semaines.
Re: marche aléatoire et conditionnement
Perso., face à un "vrai problème concret" comme le truc du robot ici, j'ai toujours eu l'impression que ça servait franchement à rien d'y connaître quoi que ce soit concernant la théorie des "chaînes de Markov" et autres "processus stochastiques" vu que les résultats de la théorie en question, dans des cas concrets comme celui là, ce qu'il "prédisent", ben y'a moyen de le montrer super facilement sans aucune théorie.
Par exemple, ici, le premier résultat qui peut sembler "un peu pointu" dont on pourrait avoir besoin, c'est celui disant que non seulement la proba. p_n que le robot soit encore sur la table au bout de n coup tend vers 0, mais que de plus, la somme des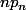 est C.V. (i.e. que l'espérance est finie).
est C.V. (i.e. que l'espérance est finie).
Sauf qu'ici, c'est une "évidence évidente" : où que soit situé le robot, il est à moins de 5 x 10cm du bord donc la proba qu'il tombe dans les 5 coups suivants est supérieure à^5) ce qui signifie que
ce qui signifie que p_n) ce qui garantie que
ce qui garantie que ) avec
avec 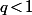 et donc assure la C.V. de toute les sommes
et donc assure la C.V. de toute les sommes 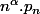 .
.
@chan79 : si tu veut faire des calculs plus simples et à la main, il te suffit de regarder ce que ça donne dans le cas où la table fait 30cm x 30cm : Dans ce cas, à symétrie prés, il n'y a que 3 positions possible du robot et on peut parfaitement faire tout les calculs à la main. En particulier, tu constatera que, à part des résultat d'algèbre linéaire, tu n'a besoin d'aucune connaissance particulière de proba. (*) pour répondre à toutes les questions que tu peut te poser concernant le bidule.
(*) Sauf bien évidement de savoir par exemple ce qu'est la définition d'une "espérance" si tu veut pouvoir calculer "l'espérance" du temps que le robot va rester sur la table. Mais la définition d'espérance vu au Lycée est largement suffisante suffisante pour conclure ici.
Par exemple, ici, le premier résultat qui peut sembler "un peu pointu" dont on pourrait avoir besoin, c'est celui disant que non seulement la proba. p_n que le robot soit encore sur la table au bout de n coup tend vers 0, mais que de plus, la somme des
Sauf qu'ici, c'est une "évidence évidente" : où que soit situé le robot, il est à moins de 5 x 10cm du bord donc la proba qu'il tombe dans les 5 coups suivants est supérieure à
@chan79 : si tu veut faire des calculs plus simples et à la main, il te suffit de regarder ce que ça donne dans le cas où la table fait 30cm x 30cm : Dans ce cas, à symétrie prés, il n'y a que 3 positions possible du robot et on peut parfaitement faire tout les calculs à la main. En particulier, tu constatera que, à part des résultat d'algèbre linéaire, tu n'a besoin d'aucune connaissance particulière de proba. (*) pour répondre à toutes les questions que tu peut te poser concernant le bidule.
(*) Sauf bien évidement de savoir par exemple ce qu'est la définition d'une "espérance" si tu veut pouvoir calculer "l'espérance" du temps que le robot va rester sur la table. Mais la définition d'espérance vu au Lycée est largement suffisante suffisante pour conclure ici.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: marche aléatoire et conditionnement

Pour une table de 30cm x 30 cm, si on note
Donc
Par exemple, l’espérance du temps qu'il va mettre à tomber, c'est la somme des
C'est à dire
qui correspond au système dont j'avais parlé dans le post du 27 Déc 2018 14:14 et qui peut bien sûr s'interpréter en terme probabiliste sur les temps moyen qu'il faut pour sortir de la table partant d'une case donnée. Sauf qu'on peut aussi ne rien interpréter du tout et faire comme je l'ai fait ici uniquement en terme d'algèbre linéaire.
Et si tu veut calculer
P.S. Et là où on voit que la théorie n'est pas forcément utile, voire même plutôt chiante dans un cas pareil, c'est que le truc décrit ci dessus ce n'est pas un processus stochastique stricto sensu vu que
Sauf que ça simplifie absolument pas les calculs, bien au contraire et comme ici, on a pas grand chose à f... des résultat théorique concernant les matrices stochastiques vu que tout se fait facilement "à la main", je vois pas l'intérêt d'introduire
Modifié en dernier par Ben314 le 29 Déc 2018, 18:32, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: marche aléatoire et conditionnement
Ben314 a écrit:Si on calcule la valeur exacte, ça donne ça :.
Le plus simple, c'est, pourde noter
le temps moyen qu'il faut pour que que le robot sorte de la table s'il est en (x,y) au départ puis de dire que :
. . .
. . .
Modulo d'utiliser les symétries, ça donne un système de 15 équations à 15 inconnues.
Salut
Pour ceux qui voudraient se lancer dans ce calcul proposé par Ben314, j'arrive au système
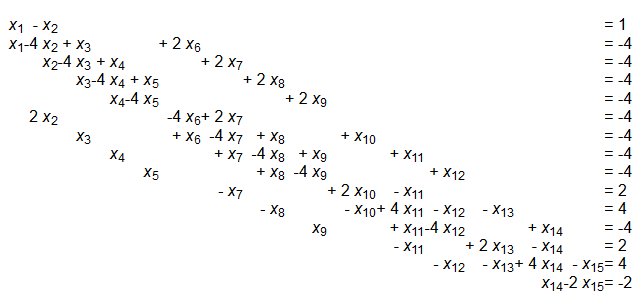
avec (x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15)=
(E(0,0),E(1,0),E(2,0),E(3,0),E(4,0),E(1,1),E(2,1),E(2,2), .... ,E(4,4))
La matrice est

On trouve bien x1=E(0,0)=
sinon, avec python
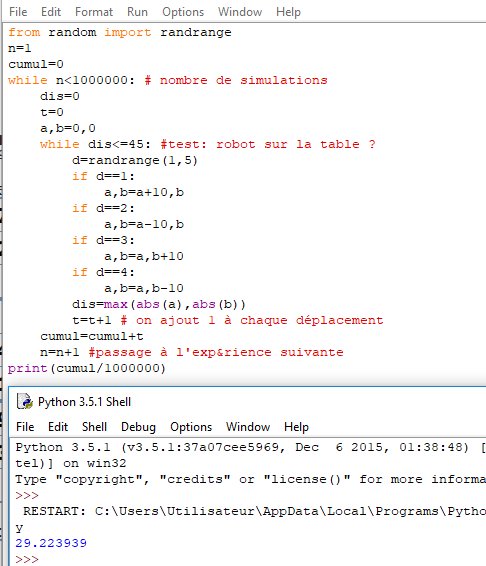
Je n'ai pas calculé la proba pour qu'il reste plus de 5 min sur la table (l'année prochaine, peut-être ...)
Ca doit être de l'ordre de 1 sur 1000000
Bon réveillon à tous !
Re: marche aléatoire et conditionnement
Bonjour pour info
Si on désigne par la probabilité du robot d'être sur la table à l'instant n alors un calcul donne
la probabilité du robot d'être sur la table à l'instant n alors un calcul donne
 si n est pair et
si n est pair et
 sinon,
sinon,
où},\frac{1}{4} \sqrt{5+2 \sqrt{5}},\frac{1}{2} \sqrt{\frac{1}{2} \left(5-\sqrt{5}\right)},\frac{1}{4} \sqrt{\frac{1}{2} \left(5+\sqrt{5}\right)},\frac{1}{4} \sqrt{\frac{1}{2} \left(5-\sqrt{5}\right)},\frac{1}{4} \sqrt{5-2 \sqrt{5}}\right\})
)
)
Les vecteurs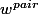 et
et 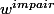 sont connus exactement mais je ne les ai pas simplifiés et restent un peu compliqués. (il y a surement encore un travail de simplification à faire
sont connus exactement mais je ne les ai pas simplifiés et restent un peu compliqués. (il y a surement encore un travail de simplification à faire
mais c'est du boulot)
Voici les valeurs de , n=1,....,40
, n=1,....,40
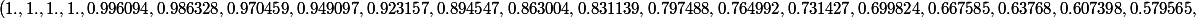
)
Donc on peut calculer la proba pour que le robot soit encore sur la table à t= 5mn=(5*60s) --->4.6217434774058617*10^{-7}
à t=30s : ---->0.353694
après à t=1mn --->0.0785755
Si on désigne par
où
Les vecteurs
mais c'est du boulot)
Voici les valeurs de
Donc on peut calculer la proba pour que le robot soit encore sur la table à t= 5mn=(5*60s) --->4.6217434774058617*10^{-7}
à t=30s : ---->0.353694
après à t=1mn --->0.0785755
Re: marche aléatoire et conditionnement
Salut
Je ne sais pas d'où viennent ces calculs mais bravo pour l'effort
Je ne sais pas d'où viennent ces calculs mais bravo pour l'effort
Re: marche aléatoire et conditionnement
Rebonjour
Finalement en faisant apparaitre uniquement les puissance paires des valeurs propres ça se simplifie bien.
Alors voilà la loi exacte.
Si n=2p,
Si n=2p+1,
avec
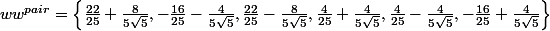
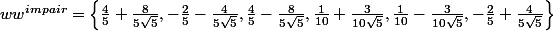
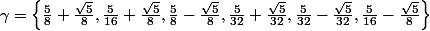 (carré des \lambda_i donnés ds le message précédent.)
(carré des \lambda_i donnés ds le message précédent.)
Une fois la loi complètement déterminée, on peut vérifier les calculs en recalculant la moyenne de la durée de vie du robot sur la table:
Après simplification on trouve:
<br />h_p(\gamma_i )+(w_i^{pair}- w_i^{impair})h_i(\gamma_i )])
où=\frac{2}{(-1+z)^2} et h_i(z)=\frac{(3-z) z}{(-1+z)^2})
On (re)trouve bien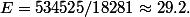
remarque: visiblement on peut encore simplifier
Finalement en faisant apparaitre uniquement les puissance paires des valeurs propres ça se simplifie bien.
Alors voilà la loi exacte.
Si n=2p,
Si n=2p+1,
avec
Une fois la loi complètement déterminée, on peut vérifier les calculs en recalculant la moyenne de la durée de vie du robot sur la table:
Après simplification on trouve:
où
On (re)trouve bien
remarque: visiblement on peut encore simplifier
Modifié en dernier par aviateur le 31 Déc 2018, 18:01, modifié 1 fois.
Re: marche aléatoire et conditionnement
Rebonjour
Pour les calculs il n'y a pas vraiment de mystère mais je ne peux pas les rapporter sur le forum: j'ai rien rédigé et c'est un peu long malgré tout.
Voici néanmoins l'idée : Tout est dans la matrice A (dont on a déjà économisé la taille, on s'est ramené à 15). Essentiellement il faut la diagonaliser. Les valeurs propres sont faciles à trouver (voir le message de @ben); là où ça se complique c'est pour les vecteur propres. Mais on peut faire de l'économie. En effet les vecteurs propres pour les vp 0 n'interviennent pas. On se retrouve avec 12 vecteurs propres. Puis avec des propriétés observées dans la matrice, on peut diviser le travail en 2 fois 6 (grosso modo c'est pour cela qu'il y a le cas n pair et n impair).
Pour avoir des expressions simples, il y a encore quelques manip à faire en particulier travailler avec les carrées des valeurs propres pour ne faire apparaitre que l'irrationnel \sqrt{5}.
Remarque tous ces calculs ne sont utiles que si on veut l'expression exacte de la loi. Sinon, si on veut des valeurs approchées avec la matrice A, ça va très vite.
Pour les calculs il n'y a pas vraiment de mystère mais je ne peux pas les rapporter sur le forum: j'ai rien rédigé et c'est un peu long malgré tout.
Voici néanmoins l'idée : Tout est dans la matrice A (dont on a déjà économisé la taille, on s'est ramené à 15). Essentiellement il faut la diagonaliser. Les valeurs propres sont faciles à trouver (voir le message de @ben); là où ça se complique c'est pour les vecteur propres. Mais on peut faire de l'économie. En effet les vecteurs propres pour les vp 0 n'interviennent pas. On se retrouve avec 12 vecteurs propres. Puis avec des propriétés observées dans la matrice, on peut diviser le travail en 2 fois 6 (grosso modo c'est pour cela qu'il y a le cas n pair et n impair).
Pour avoir des expressions simples, il y a encore quelques manip à faire en particulier travailler avec les carrées des valeurs propres pour ne faire apparaitre que l'irrationnel \sqrt{5}.
Remarque tous ces calculs ne sont utiles que si on veut l'expression exacte de la loi. Sinon, si on veut des valeurs approchées avec la matrice A, ça va très vite.
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

