Limites en a de fonction irrationnelles ,1èreS

[Kiritsugu]

Bonsoir je suscite votre aide pour quelques exercices sur les limites qui je n'arrive pas à , j'ai tout tenté(Factorisation ,expression conjuguée) mais rien , voici les exercices t merci d'avance :
Calculer :
1.
2. et
3.
Ah et s'il vous plait si vous avez un formule pour résoudre ce genre de cas rapidement je serai heureux d'en avoir la connaissance. Merci.

[chan79]

salut
Pour la 1, multiplie en haut et en bas par la quantité conjuguée du numérateur et par la quantité conjuguée du dénominateur.

Petite remarque:
Tu as fait une étourderie:
On dit: "je sollicite votre aide" et non "je suscite votre aide".
Le sens n'est pas le même; il ne faudrait pas se tromper dans une lettre officielle (envoi de CV ou autre )

[Kiritsugu]

Ah oui merci pour ta remarque j'hesitais entre les deux expression sinon vous n'aurez pas de solution pour la 2 et la 3?

[chan79]

je ne vois pas de forme indéterminée

[laetidom]

Ah oui merci pour ta remarque j'hesitais entre les deux expression sinon vous n'aurez pas de solution pour la 2 et la 3?

Bonjour,

2) pas de difficultés particulière dans le calcul qui donne au final :

si x --> 2- alors f(x) -->

si x --> 2+ alors f(x) -->

que l'on peut vérifier aisément sur le graphique : http://www.cjoint.com/c/FBbnzFysrO7

[zygomatique]

salut

1/ ...

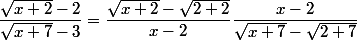
2/ ....

3/ revoir ton énoncé ...

[Kiritsugu]

Ok merci j'avais finalement trouvé.