Alors bonjour jai deux limites d'exponentielles à faire mais je ne comprend pas grand chose aux limites et à part trouver un résultat à la calculatrice je n'ai aucune piste alors voici les deux limites je suis pourtant sur que ce n'est pas si compliqué
A)(x^2-2x+1)e^-x
B)e^x-x^2+x+1
Merci d'avance à ceux qui m'aideront bon après midi
Limites exponentielle
7 messages
- Page 1 sur 1
Re: Limites exponentielle
Quand
Au voisinage de l'infini, l'exponentielle l'emporte sur toute fonction polynôme
etc ....
Re: Limites exponentielle
J'essaye merci beaucoup pour ton aide je comprend pas par contre la première étape pour le changement d'écriture
Re: Limites exponentielle
Simple factorisation par  :
: 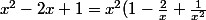)
Au v. de l'infini un polynôme est équivalent à (se comporte comme) son terme de plus haut degré.
Au v. de l'infini un polynôme est équivalent à (se comporte comme) son terme de plus haut degré.
Re: Limites exponentielle
J'ai supposé acquis que 
mais je me rends compte que les cours ne mentionnent habituellement que la limite de est 0
est 0
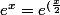^2}) et
et 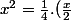^2)
En posant ,
, 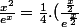^2=\frac14. \frac{X}{e^X}) qui tend vers 0 quand x et donc X tendent vers
qui tend vers 0 quand x et donc X tendent vers 
mais je me rends compte que les cours ne mentionnent habituellement que la limite de
En posant
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
