Limites fonction exponentielle

[Norma]

Le problème de fond que j'ai c'est qu'au final je ne comprends pas ce que je fais ni pourquoi je le fais... Je ne comprends pas à quoi cela me sert d'observer comment se comportent des courbes... ce n'est pas une matière assez représentative "concrète" pour moi.. Ducoup j'applique et reproduit des calculs et formules mais sans en voir l'intérêt ni le pourquoi, c'est pour ça je pense que je ne fais pas les liens.

Je ne comprends pas non plus très souvent les questions, comme celle qui suit cet exercice :

Vérifier que pour tout réel x,
En déduire la limite de f(x) quand x tend vers

Alors j'ai bien compris que c'est la même fonction mais factorisée, (non?).. mais je ne comprends pas ce qu'on me demande d'en faire.. déduire la limite au final cela ne me semble pas trop compliqué puisque je l'ai fais plus haut avec x qui tend vers

[laetidom]

Le problème de fond que j'ai c'est qu'au final je ne comprends pas ce que je fais ni pourquoi je le fais... Je ne comprends pas à quoi cela me sert d'observer comment se comportent des courbes... ce n'est pas une matière assez représentative "concrète" pour moi.. Ducoup j'applique et reproduit des calculs et formules mais sans en voir l'intérêt ni le pourquoi, c'est pour ça je pense que je ne fais pas les liens.

Je suis un peu comme toi, en maths j'ai besoin, quand c'est possible et bien souvent cela doit l'être si l'on s'en donne la possibilité, de traduire des calculs par un schéma, un graphique (même à main levée), ça me parle davantage !!

Je ne comprends pas non plus très souvent les questions, comme celle qui suit cet exercice :

Vérifier que pour tout réel x, factoriser permet souvent de conclure
En déduire la limite de f(x) quand x tend vers si tu réussi à avoir des fractions du type "petit sur grand" quand x tend vers l'infini et bien la fraction s'annule ! : 1/100000000000000000 ---> 0.0000000001 !! (pratique pour simplifier)

Alors j'ai bien compris que c'est la même fonction mais factorisée, (non?).. mais je ne comprends pas ce qu'on me demande d'en faire.. déduire la limite au final cela ne me semble pas trop compliqué puisque je l'ai fais plus haut avec x qui tend vers

Il ne faut pas se décourager, lorsque l'on maitrise un certain nombre de choses, les maths peuvent être jubilatoires, même avec un niveau modeste, ce qui est mon cas ! Et les maths ouvrent (ou l'inverse ? . . .) à la philosophie (l'amour de la sagesse !!), c'est pourquoi tous les grands Grecs sont au minimum les 2 à la fois (Matheux-Philosophes) !!!!!!

[Norma]

Mais je dois conclure quoi???? Que la première est égale à la deuxième ? Mais pourquoi ? Comment?? Je commence sérieusement à me lasser de rien comprendre

[laetidom]

Mais je dois conclure quoi???? Que la première est égale à la deuxième ? Oui !! Mais pourquoi ? Parce que la forme factorisée permet de lever une indétermination que tu n'avais pas pour - inf mais qui apparaît pour + inf Comment?? Je commence sérieusement à me lasser de rien comprendre

Avec la forme développée de f(x) (celle du départ) :

lim en : on avait 0 - 0 + 2 =

lim en : on aurait + 2
or est une forme indéterminée ! Donc il faut une forme factorisé de f(x).

[Norma]

Alors ok, comment on démontre qu'une forme factorisée est égale à une autre??

Pour la limite de la forme factorisée j'ai alors :





Donc

[Norma]

Mais je dois conclure quoi???? Que la première est égale à la deuxième ? Oui !! Mais pourquoi ? Parce que la forme factorisée permet de lever une indétermination que tu n'avais pas pour - inf mais qui apparaît pour + inf Comment?? Je commence sérieusement à me lasser de rien comprendre

Avec la forme développée de f(x) (celle du départ) :

lim en : on avait 0 - 0 + 2 =

lim en : on aurait + 2
or est une forme indéterminée ! Donc il faut une forme factorisé de f(x).

Pour ce n'est pas + inf? les deux parties de la fraction ont des limites de +inf non?

[laetidom]

exemples saisis à la calculatrice :

100 / e^100 = 3,72 . 10^-42 (tend vers 0)

2 / e^100 = 7,44 . 10^-44 (tend vers 0)

[laetidom]

Pour ce n'est pas + inf? les deux parties de la fraction ont des limites de +inf non? qd x ---> + inf alors e^x croit beaucoup plus rapidement que x :

exemples saisis à la calculatrice :

100 / e^100 = 3,72 . 10^-42 (tend vers 0)[/color]

[Norma]

ok d'accord, mais donc au final j'ai pas encore démontré dans tout ça que les fonction sont équivalentes

[laetidom]

ok d'accord, mais donc au final j'ai pas encore démontré dans tout ça que les fonctions sont équivalentes

Que veux-tu démontrer de plus ? Tu l'as factorisée donc elle est équivalente !!

[Norma]

Ben c'est la question : vérifier que pour tout réel x f(x)= f(x) factorisée

[laetidom]

Ben c'est la question : vérifier que pour tout réel x f(x)= f(x) factorisée

Là je ne vois pas ce que l'on peut ajouter, je sèche, désolé !

Si un autre intervenant peut renseigner Norma, merci pour elle !

[Norma]

Merci pour tout ça!! Effectivement l'idée du canapé est on ne peut plus explicite... ça parait bête mais pour des gens comme moi qui n'y comprennent rien ou du moins pas grand chose... ça fait beaucoup de traduire avec des exemples simples. Je pars donc calculer ?? je me pencherai dessus demain


Je dois ensuite calculer f'(x), je suis parti de la première fonction non factorisée et j'ai :
C'est possible?

On me demande ensuite de vérifier que
Ce qui me donne Donc plausible avec ce que j'ai plus haut.

Résoudre dans R f'(x)=0 (je le ferais demain)

MERCI ENCORE! Sans vous tous j'aurais lâché le morceau depuis bien longtemps!

[Lostounet]

Salut,

Je pense que le plus important, c'est de vraiment comprendre pourquoi on est en train de faire ce qu'on fait !

Concernant le "f(x) factorisée" ou pas factorisée:
Imagine (exemple bateau) un canapé-lit dans ton salon. Si tu as des invités, il faut choisir laquelle des deux formes est la plus adaptée à la situation: on va passer en mode "canapé" quand on doit installer plusieurs personnes, et en mode "lit" le soir, pour dormir.

On choisit donc toujours, quand cela est possible, d'adapter l'objet à l'usage que l'on veut en faire. Et en maths, c'est exactement la même chose.

Je vais te poser deux questions:
1) Peux-tu trouver un nombre tel que si j'ajoute à ce nombre son carré, je trouve 6 ?

2) Si je multiplie un nombre (appelons-le "a") par un autre nombre disons b, je trouve 0 (ie: ab=0). Que vaut a ou b?


Normalement, tu devrais préférer répondre à la deuxième question: un des deux nombres est donc forcément nul ! Soit a=0, soit b =0 pour avoir ab = 0 !
Tout cela pour te dire que, étant donné un objet mathématique (une expression littérale), on peut préférer le mettre sous une autre forme afin de répondre plus simplement aux questions que l'on se pose.
Et une des techniques que l'on peut adopter, c'est d'utiliser pour une même expression: soit la forme développée, soit la forme factorisée.

Pour répondre donc à la première question que je t'ai posée, tu cherches un nombre inconnu x tel que
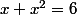
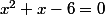
ou bien, de manière tout à fait équivalente en retranchant 6 des deux cotés . Cette équation est difficile à résoudre, mais si je te propose d'écrire la quantité x^2 + x - 6 autrement, en constatant que x^2 + x - 6 = (x - 2)(x + 3) (à justifier pourquoi c'est vrai pour tout nombre x!)

Alors tu cherches en fait x tel que
Ceci est un produit de deux nombres a et b, tel que ab = 0 alors forcément a = 0 ou bien b = 0 !
Cela signifie que x - 2 = 0 ou bien x + 3=0, donc x = 2 ou bien x = -3.

Cette "magique transformation" de la quantité en apparence compliquée x^2 + x - 6 en une autre forme de produit (dite factorisée) (x - 2)(x + 3) est en fait une factorisation, qui permet de trouver la valeur de x plus simplement.

Si tu souhaites revoir ces notions de "développement" et "factorisation", je t'invite à relire cette discussion ici:
college-primaire/developper-factoriser-t120839.html

Ces deux techniques, permettent souvent de répondre à plusieurs questions concernant une expression: tu en as fait l'expérience ici sur le calcul des limites. Des fois on ne connait pas directement la limite d'une expression qu'en la factorisant... (on y reviendra)


(Donc non tu ne dois pas "remplacer par une valeur triviale" )

[Norma]

Merci pour tout ça!! Effectivement l'idée du canapé est on ne peut plus explicite... ça parait bête mais pour des gens comme moi qui n'y comprennent rien ou du moins pas grand chose... ça fait beaucoup de traduire avec des exemples simples. Je pars donc calculer ?? je me pencherai dessus demain


Je dois ensuite calculer f'(x), je suis parti de la première fonction non factorisée et j'ai :
C'est possible?

On me demande ensuite de vérifier que
Ce qui me donne Donc plausible avec ce que j'ai plus haut.

Résoudre dans R f'(x)=0 (je le ferais demain)

MERCI ENCORE! Sans vous tous j'aurais lâché le morceau depuis bien longtemps!

[laetidom]

Bonjour,

Effectivement l'idée du canapé est on ne peut plus parlante !...

On a ok !,

Si on remarque que x = 0 est solution évidente car

alors on peut faire la division euclidienne de par soit pour obtenir ,

ce qui signifie que l'on peut écrire que et comme tu l'as très bien fait pour vérifier, en développant cette forme factorisée obtenue tu retrouves la forme initiale ! :



===========================================
Ensuite (chercher l'abscisse là où la courbe a une tangente de pente nulle donc une tangente horizontale) :

Soit , faut encore remarquer la solution " évidente " . . .

Soit , là tout de suite on se dit : ou d'où ou



Bonne journée @ tous !

[Norma]

Hello, merci pour ses piste mais je ne comprends pas pourquoi la division euclidienne? Pourquoi avec ces termes et qu'est ce qu'elle montre?

Et pour répondre à la question Vérifier que pour tout x réel, f(x)=f(x) factorisée, ne dois-je pas calculer en lien avec ce que disait Lostounet?


Merci

[laetidom]

Hello,

Hello, merci pour ses piste mais je ne comprends pas pourquoi la division euclidienne? Pour factoriser une expression donc pour tenter de la résoudre plus facilement Pourquoi avec ces termes et qu'est ce qu'elle montre?
Merci

[Norma]

D'accord,

J'ai tenté de faire le calcul f(x)=0:

Donc est impossible

Alors il reste




Mais ensuite ?

[laetidom]

C'est ou . . . ?