Bonjour ! J'aurais besoin de petit coup de main dans le calcul d'une limite. Je dois résoudre plusieurs limites indéterminée par 1^en l'infini. Je dois utiliser le ln mais je ne sais plus comment. La voici:
lim ((x-1)/(x+1))^x
x;)+ l'infini
Jespère que l'on pourra m'aider et merci d'avance.
Limites exponentielle
8 messages
- Page 1 sur 1
Max9500 a écrit:Bonjour ! J'aurais besoin de petit coup de main dans le calcul d'une limite. Je dois résoudre plusieurs limites indéterminée par 1^en l'infini. Je dois utiliser le ln mais je ne sais plus comment. La voici:
lim ((x-1)/(x+1))^x
x;)+ l'infini
Jespère que l'on pourra m'aider et merci d'avance.
Bonsoir,
je te propose une solution mais je me demande s'il n'y a pas plus rapide ...
Changement de variable : X = 1/x. On cherche donc la limite en 0 de :
Dénominateur : la limite en 0 de
Numérateur : même chose qu'au dénominateur, mais en faisant une nouveau changement de variable X'=-X. On trouve e^{-1}
Conclusion, ta limite vaut
Salut,
Perso, quand j'ai une indétermination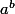 où a->1 et b->oo, je réfléchis pas trop : je l'écris
où a->1 et b->oo, je réfléchis pas trop : je l'écris 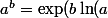)) puis, du fait que a->1, je fait apparaitre le rapport
puis, du fait que a->1, je fait apparaitre le rapport }{a-1}=\frac{\ln(a)-\ln(1)}{a-1}) qui tend vers
qui tend vers =\frac{1}{1}=1) .
.
Ca donne donc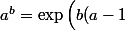\frac{\ln(a)}{a-1}\Big)) donc si
donc si ) tend vers une limite L alors
tend vers une limite L alors 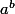 tend vers
tend vers ) .
.
Application numérique : si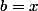 et
et  alors
alors =x\frac{(x-1)-(x+1)}{x}=-2) donc a^b tend vers
donc a^b tend vers )
Perso, quand j'ai une indétermination
Ca donne donc
Application numérique : si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Salut,
Perso, quand j'ai une indéterminationoù a->1 et b->oo, je réfléchis pas trop : je l'écris
puis, du fait que a->1, je fait apparaitre le rapport
qui tend vers
.
Ca donne doncdonc si
tend vers une limite L alors
tend vers
.
si
et
alors
donc a^b tend vers
Il y avait donc nettement plus simple
zygomatique a écrit:salut
on peut aussi remarquer que
et si nécessaire l'écrire même
lorsqu'on sait que
sinon le plus méthodique et classique est bien sur de faire comme ben314
:lol3:
En effet zygomatique ! C'est ta méthode que j'aurais faite, plus rapide et plus léchée
La méthode de Ben314 ne me serait jamais venue à l'idée alors qu'elle est pourtant tellement logique
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 148 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
