Limite en + l'infini
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
ArKange635
- Messages: 9
- Enregistré le: 22 Sep 2010, 19:02
-
 par ArKange635 » 22 Sep 2010, 19:06
par ArKange635 » 22 Sep 2010, 19:06
Bonjour, je dois trouver la limite en + l'infini de
= \frac{\sqrt{x-1}}{x-3})
j'ai essayé la factorisation, mais cela ne donne rien... :triste:

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 22 Sep 2010, 19:21
par Sa Majesté » 22 Sep 2010, 19:21
Salut
Tu mets

en facteur au numérateur et x en facteur au dénominateur
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 22 Sep 2010, 19:25
par Mortelune » 22 Sep 2010, 19:25
ArKange635 a écrit:Bonjour, je dois trouver la limite en + l'infini de
= \frac{sqrt(x-1)}{x-3})
j'ai essayé la factorisation, mais cela ne donne rien... :triste:
Pour un x assez grand pour que ça ne pose pas de problème (ce qui sera le cas comme on cherche une limite en

). On peut prendre x>100.
Alors on va diviser le numérateur et le dénominateur par x-1 pour se ramener à quelque chose qui sera peut être plus connu.
-
ArKange635
- Messages: 9
- Enregistré le: 22 Sep 2010, 19:02
-
 par ArKange635 » 22 Sep 2010, 19:55
par ArKange635 » 22 Sep 2010, 19:55
Merci beaucoup! Je n'avais mis que x en facteur au numérateur et cela ne m'aidait pas beaucoup!
-
ArKange635
- Messages: 9
- Enregistré le: 22 Sep 2010, 19:02
-
 par ArKange635 » 22 Sep 2010, 21:14
par ArKange635 » 22 Sep 2010, 21:14
Oula... je me suis trompé. Je ne vois pas... ça marchait pour
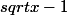
mais du coup je ne vois pas pour

. Sinon je viens de penser a diviser numérateur et dénominateur par

. On tombe sur du
(sqrt{x-1})})
et là on trouve la limite= à 0. Ou alors j'ai tout faux

-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 22 Sep 2010, 21:17
par Mortelune » 22 Sep 2010, 21:17
Bonsoir,
La limite est bien nulle et la technique qui t'a été donnée marche dans les 2 cas que tu cites. Même s'il en existe d'autre. Mais si en divisant par
)
tu trouve la limite alors c'est que tu aurais pu la voir immédiatement.
-
ArKange635
- Messages: 9
- Enregistré le: 22 Sep 2010, 19:02
-
 par ArKange635 » 22 Sep 2010, 21:18
par ArKange635 » 22 Sep 2010, 21:18
La voir immédiatement... On tombe sur un cas de forme indéterminée non?
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 22 Sep 2010, 21:34
par Mortelune » 22 Sep 2010, 21:34
Non je viens de jeter un coup d'oeil à ce que tu as écrit, tu as mal divisé par

donc tu ne la trouvais pas immédiatement, dans le cas dont je te parlais tu serais tombé sur l'inverse de l'inverse de ta fonction initiale (ça fait beaucoup d'inverse ^^)
-
ArKange635
- Messages: 9
- Enregistré le: 22 Sep 2010, 19:02
-
 par ArKange635 » 22 Sep 2010, 21:37
par ArKange635 » 22 Sep 2010, 21:37
Donc au final j'ai faux?
-
ArKange635
- Messages: 9
- Enregistré le: 22 Sep 2010, 19:02
-
 par ArKange635 » 22 Sep 2010, 21:45
par ArKange635 » 22 Sep 2010, 21:45
Mortelune a écrit: tu as mal divisé par

C'est là que je n'ai pas compris ce que tu voulais dire ^^'

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 22 Sep 2010, 21:49
par Sa Majesté » 22 Sep 2010, 21:49
Tu as
= \frac{\sqrt{x-1}}{x-3} = \frac{\sqrt{x}\sqrt{1-\frac{1}{x}}}{x \left(1-\frac{3}{x}\right)} = \frac{\sqrt{1-\frac{1}{x}}}{\sqrt{x} \left(1-\frac{3}{x}\right)})
-
ArKange635
- Messages: 9
- Enregistré le: 22 Sep 2010, 19:02
-
 par ArKange635 » 22 Sep 2010, 21:54
par ArKange635 » 22 Sep 2010, 21:54
Ah voila merci! Je m'embrouillais avec ces racines mais j'ai enfin compris ^^
Merci beaucoup et bonne soirée!
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 22 Sep 2010, 21:57
par Mortelune » 22 Sep 2010, 21:57
ArKange635 a écrit:C'est là que je n'ai pas compris ce que tu voulais dire ^^'
Quand tu agis sur une fonction pour conserver l'égalité tout ce que tu lui feras subir reviendra à la multiplier par 1 ou à lui ajouter 0, or ce que tu avais fait était simplement une division qui te faisait changer de fonction, donc c'était faux.
-
ArKange635
- Messages: 9
- Enregistré le: 22 Sep 2010, 19:02
-
 par ArKange635 » 22 Sep 2010, 22:00
par ArKange635 » 22 Sep 2010, 22:00
D'accord ^^ merci pour l'info, ça me sera très utile en DS (pour éviter les bourdes monumentales ^^')
-
ArKange635
- Messages: 9
- Enregistré le: 22 Sep 2010, 19:02
-
 par ArKange635 » 22 Sep 2010, 22:09
par ArKange635 » 22 Sep 2010, 22:09
Autre question, grâce à la limite déterminée précédemment, peut-on en déduire une asymptote horizontale en y=0 ou non? Je sais qu'il y en a une verticale en x=3 mais je ne suis pas sur pour y=0...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 133 invités
= \frac{\sqrt{x-1}}{x-3})
