[TS] Limite et asymptotes

[Ericovitchi]

D'abord 1/(2 pi) = 0.159 ensuite ça n'est pas le bon résultat parce que les points d'intersection entre C et D2 c'est les solutions de sin(1/x)=-1 donc 1/x=(3pi/2) + k2pi le premier est donc en 2/3pi qui vaut 0.212 donc ça marche

[tite_prune]

D'accord. Donc je vais essayer de faire avec D1 parce que pour le moment je fais que des erreurs.
D1=x/3
f(x)=D1
sin(1/x)=1
sin( /2 (+2k)=1
(1/x)= /2 (+2k le 1er x : x=2/=0.64 ( à peu près) , ce qui est bien compris entre 0 et 0.7.
Je crois que cette fois j'ai compris
Est ce juste?

[tite_prune]

Je remonte le sujet pour quand vous reviendrez , parce la il coule ^^

[Ericovitchi]

oui, je vois que tu avances

[tite_prune]

a ben ça me fais plaisir déjà d'avoir compri la démarche.
Ensuite pour la question 2b faut-il passer par une récurrence?

[Ericovitchi]

Pour démontrer 0 0,01x ?
non je ne vois pas bien sur quoi tu veux faire de la récurrence.

C'est plus simple que ça. regarde la fonction sin(1/x). Quand x va augmenter elle va décroître vers 0. Donc sa plus grande valeur sera sin(1) (puisque on te dit que x>=1) et sin (1 radian) = 0.84 justement

f(x)-x/3 = x/(2+ sin (1/x)) - x/3 = x(1-sin(1/x)) / (3(2 + sin(1/x)) )
Essaye de minorer ça. le (1-sin(1/x) ) est toujours supérieur à 1-0.85=0.15
On peut majorer le dénominateur (donc minorer la fraction) par 3(2+0.85)=8.55
donc f(x)-x/3 > 0.15x /8.55 ~ 0.175 x > 0.01x

[tite_prune]

Je ne comprend pas bien quand vous dites majorer le dénominateur. Sinon ce que vous avez fait est très claire et j'ai bien compri les étapes mais c'est cette formulation majorer le dénominateur que je n'avais jamais rencontré

[Ericovitchi]

je veux trouver quelque chose de plus petit que notre fraction.
Donc pour faire ça, je peux remplacer le numérateur par quelque chose de plus petit 1-sin(1/x) par 0.85
Et je peux remplacer le dénominateur par quelque chose de plus grand (ça fait aussi diminuer la fraction)
ici (3(2 + sin(1/x)) par 8.55

[tite_prune]

A d'accord, ensuite pour les questions suivantes je crois que je saurais faire.Merci beaucoup en tout cas
Par contre cela vous dérange-t-il de m'aider pour un nouvel exercice?

[tite_prune]

bon je poste on sait jamais^^
soit m un nombre réel et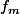 la fonction définie par: 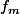(x)=.On note 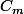la courbe représentative de 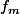dans un rapère du plan.
1)Prouver que la fonction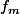 est définie pour des valeurs de x dont la valeur absolue est suffisamment grande.
--->ici j'ai fais:
x^2+2mx-1>0 car une racine n'est jamais négative , donc j'ai fait
=4-4(-1)=8
d'où les racines sont =-1- et =-1+
fm(x) est donc définie sur ]-;-1-] U [-1+;+[
j'aimerai savoir si cette question est juste

[Le Chaton]

Bonsoir , il est passé ou ton "m" ?

b²-4ac ça te donne quoi ? ! ( en remarquant que b=2m)

[tite_prune]

Salut Le chaton!!
Ben je l'ai ommi parce que je savais pas vraiment quoi en faire mais si je le laisse j'ai:
4m²-4(-1*1)=4m²-4
et donc comme =-m- et=-m+

[Le Chaton]

Salut Le chaton!!
Ben je l'ai ommi parce que je savais pas vraiment quoi en faire mais si je le laisse j'ai:
4m²-4(-1*1)=4m²-4
et donc comme =-m- et=-m+

(-4)*(-1) ça fait combien ? est ce que ça fait -4 ? ... ? Donc quelle est le signe de delta ?Ensuite ouest passé ton 4 ? sous la racine ??? .////

[tite_prune]

oui ça fait 4m²+4 donc delta positif
mais après pour les x
j'ai x=-2m+/2 =-2m+/2=-2m+2/2=2(-m+)/2=-m+
x=-m- avec le même raisonnement