Bonsoir,
J’ai un petit problème de suite
(terminale spe)
je dois passer de
un<r/2 <-> uN1 +….+un <r/2
en sachant que
n>(ou égal) N1
ma question porte sur le fait de transformer une suite en une somme de plusieurs terme de cette suite.
Merci
Lien entre somme de suite et suite
6 messages
- Page 1 sur 1
Re: lien entre somme de suite et suite
Bonjour,
pourrais-tu donner ton énoncé complet car c'est incompréhensible!
pourrais-tu donner ton énoncé complet car c'est incompréhensible!
Re: lien entre somme de suite et suite
alors oui :
le but est de démontrer le théorème de Cesaro, qui converge vers une limite l
et de montrer que pour tout r>0 | cn |<r apcr
on a démontré que un< r/2
et que cn = u1 +… +uN1-1/n + uN1+…+un/n
pour tout n>(=) N1
maintenant il faut expliquer pourquoi :
uN1+…+un/n <(=) r/2
voilà merci beaucoup
le but est de démontrer le théorème de Cesaro, qui converge vers une limite l
et de montrer que pour tout r>0 | cn |<r apcr
on a démontré que un< r/2
et que cn = u1 +… +uN1-1/n + uN1+…+un/n
pour tout n>(=) N1
maintenant il faut expliquer pourquoi :
uN1+…+un/n <(=) r/2
voilà merci beaucoup
Re: lien entre somme de suite et suite
Quand tu écris cn = u1 +… +uN1-1/n + uN1+…+un/n
Je dois faire un gros effort pour lire.
Concentrons nous sur uN1-1/n
C'est u(N1) -1/n ou bien u(N1-1)/n ?
ou mieux :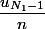
Pourquoi certains termes sont divisés par n, et pas les autres ?
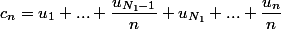
Je pense que la question elle-même nécessite moins d'une minute de réflexion, mais déchiffrer la question est trop compliqué.
Je dois faire un gros effort pour lire.
Concentrons nous sur uN1-1/n
C'est u(N1) -1/n ou bien u(N1-1)/n ?
ou mieux :
Pourquoi certains termes sont divisés par n, et pas les autres ?
Je pense que la question elle-même nécessite moins d'une minute de réflexion, mais déchiffrer la question est trop compliqué.
Re: lien entre somme de suite et suite
Bonjour
Oui lycéen95 c'est vraiment du décryptage...
je suppose que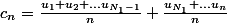
Oui lycéen95 c'est vraiment du décryptage...
je suppose que
Re: lien entre somme de suite et suite
J'ai oublié des +
je suppose que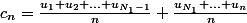
Faut il majorer la deuxème fraction sachant que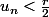 si n>=
si n>=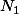 ?
?
je suppose que
Faut il majorer la deuxème fraction sachant que
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
