Bonjour Donc voila je suis e train de faire un exercice sur les dérivés je sais que P est une parabole d'equation y=x²
Je fais une figure sur [-4;4] avec a=1 et b= -3
La question est Déterminer les tangentes Ta et Tb !
Voila comment jai fait :
Jai pris la fonction f(x)= x²
Donc f '(x)= 2x
Je suis pas sur de moi pour ca je sais pas si la droite d'equation y vaut f(x)
Et jai continué le problème donc je sais que :
Pour A, y= f '(a)-(x-a)+f(a)
= 2(x-1)+1
= 2x-1
Pour B, y= f '(b)-(x-b)+f(b)
= 6(x-3)+9
= 6x-9
Est ce que j'ai raison ?? Merci davance de votre aide !!
Les dérivés
8 messages
- Page 1 sur 1
Salut,
c'est pas y=f'(a)-(x-a)+f(a) la formule c'est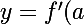\times(x-a)+f(a))
sinon pour a=1c'est bon quand même
pour b=-3 c'est pas bon
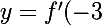\times(x+3)+f(-3))
Je suis pas sur de moi pour ca je sais pas si la droite d'equation y vaut f(x)
Et jai continué le problème donc je sais que :
Pour A, y= f '(a)-(x-a)+f(a)
= 2(x-1)+1
= 2x-1
Pour B, y= f '(b)-(x-b)+f(b)
= 6(x-3)+9
= 6x-9
c'est pas y=f'(a)-(x-a)+f(a) la formule c'est
sinon pour a=1c'est bon quand même
pour b=-3 c'est pas bon
Les dérivés
Oui c'est vrai ! Excusez moi c des erreurs de frappe que j'ai commis mais c'est ce que je voulais dire y= f '(a)(x-a)+f(a) et b c'etait b=3 Je m'atais trompé ! Donc normalement c'est bon ! Après ya une question c'est
determiner les coordonnées du point J intersection de Ta et Tb
Je sais pas comment on calcule les coordonnées , je sais que avec les fonctions est ce c'est comme ca xJ = xA+xB/2 et yJ= yA+yB/2 ?? Merci davance !
Mais si c ca je vois pas comment je saurais que vaut xA , xB , yA et yB car c lintersection des tangentes .
Pouverz vous maider ??
Merci davance !!
determiner les coordonnées du point J intersection de Ta et Tb
Je sais pas comment on calcule les coordonnées , je sais que avec les fonctions est ce c'est comme ca xJ = xA+xB/2 et yJ= yA+yB/2 ?? Merci davance !
Mais si c ca je vois pas comment je saurais que vaut xA , xB , yA et yB car c lintersection des tangentes .
Pouverz vous maider ??
Merci davance !!
Les dérivés
Ah oui et ca me donne x=2 , e en remplacant dans Ta :
y=f'(a)(x-a)+f'(a)
y=2(2-1)+1
y=3
Donc en fait les coordonnées de j sont (x:2) et (y:3) c ca ??
Je comprends mieux pourquoi la question d'après c'est determiner les coordonnées dedu milieu I de [AB] ? Pour cela je dois utiliser :
xI=xA+xB/2 yI=yA+yB/2
=1+3/2 =3+3/2
=2 =3
C'est ca ??
Merci davance de votre aide Fonfon c'est très gentil à vous !!
y=f'(a)(x-a)+f'(a)
y=2(2-1)+1
y=3
Donc en fait les coordonnées de j sont (x:2) et (y:3) c ca ??
Je comprends mieux pourquoi la question d'après c'est determiner les coordonnées dedu milieu I de [AB] ? Pour cela je dois utiliser :
xI=xA+xB/2 yI=yA+yB/2
=1+3/2 =3+3/2
=2 =3
C'est ca ??
Merci davance de votre aide Fonfon c'est très gentil à vous !!
Ah oui et ca me donne x=2 , e en remplacant dans Ta :
y=f'(a)(x-a)+f'(a)
y=2(2-1)+1
y=3
ok
Je comprends mieux pourquoi la question d'après c'est determiner les coordonnées dedu milieu I de [AB] ? Pour cela je dois utiliser :
xI=xA+xB/2 yI=yA+yB/2
c'est bien ces formules qu'il faut utiliser apres ne connaissant pas A et B je ne sais pas si les calculs sont corrects mais je pense que c'est bon
Les dérivés
Ben en fait pour les calculs daprès lénoncé je sais que a=1 et b=3
Donc pour moi xA= 1 et xB = 3
Après pour trouver yA et yB jutilise
yA=f'(a)(x-a)+f'(a) et yB= f '(b)-(x-b)+f(b)
Est ce bien ces trucs la qu'il faut utiliser ?? Si c'est ca mes résultats sont justes !!
Merci davance de ton aide fonfon !
Donc pour moi xA= 1 et xB = 3
Après pour trouver yA et yB jutilise
yA=f'(a)(x-a)+f'(a) et yB= f '(b)-(x-b)+f(b)
Est ce bien ces trucs la qu'il faut utiliser ?? Si c'est ca mes résultats sont justes !!
Merci davance de ton aide fonfon !
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
