Intégrale et fonction paire ou impaire

par **egan** » 25 Aoû 2009, 11:11

Salut,
J'ai pensé à quelque chose, j'aimerais avoir votre avis.

Soit f une fonction définie sur un intervalle I (ouvert ou fermé ?) et centré sur 0, et a un réel strictement positif appartenant à I.
Si f est paire, alors

.
Si f est impaire, alors

.

Ca me paraît juste quand on se visualise le graphique de telles fonctions mais j'ai du mal à trouver une démo correcte.
@+ Boris.

par **sky-mars** » 25 Aoû 2009, 11:13

Salut
1) un changement de variable suffit amplement

ou

2) utiliser chasles

par **Edward** » 25 Aoû 2009, 11:13

Essaye un changement de variable x = -t

par **egan** » 25 Aoû 2009, 11:17

J'avais essayé ça mais ça me semblait pas terrible parce que si on fait un changement de variable sur une des intégralles il faut le faire sur la deuxième non ?

par **sky-mars** » 25 Aoû 2009, 11:20

Non si tu l'applique sur une seule intégrale pour retrouver la deuxième ( c'est a dire l'égalité) ;)

par **egan** » 25 Aoû 2009, 15:57

Cas de la fonction paire:

Mais j'arrive pas à finir là.

par **mathelot** » 25 Aoû 2009, 16:02

egan a écrit:Si f est paire, alors .

d'où F(a)=-F(-a)
la primitive qui s'annule en 0 est impaire.

par **Nightmare** » 25 Aoû 2009, 16:52

Bonjour,

f n'est nulle part supposée continue ! Il faut oublier changements de variable et primitives.

par **struett** » 25 Aoû 2009, 17:37

Nightmare a écrit:Bonjour,

f n'est nulle part supposée continue ! Il faut oublier changements de variable et primitives.

Bonjour à tous,

Je vais peut-être dire une énormité, mais... Si f est intégrable, elle est continue, nan? Il me semble qu'on définit l'intégrale que pour des fonctions continues... :cry:

par **egan** » 25 Aoû 2009, 20:21

J'ai oublié de mettre dans les hypothèses de départ que f était continue. ;)
Je bloque sur la démo, j'arrive pas à trouver le bon résultat.

par **girdav** » 25 Aoû 2009, 20:23

struett a écrit:Bonjour à tous,

Je vais peut-être dire une énormité, mais... Si f est intégrable, elle est continue, nan? Il me semble qu'on définit l'intégrale que pour des fonctions continues...

Bonjour.
Non, les fonctions en escalier sont intégrables bien que pas toujours continues.

par **girdav** » 25 Aoû 2009, 20:25

egan a écrit:Cas de la fonction paire:

Mais j'arrive pas à finir là.

Normal, tu as mal changé les bornes. Avec

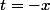
, quand

vaut

, et quand

vaut

.

par **egan** » 25 Aoû 2009, 20:34

Ah ok donc c'est ça:

Mais j'ai l'impression que ça coince quelque part. Moi je veux montrer:

et je tombe sur

. Est-ce que l'on peut considérer que cela revient au même en disant que les variables sont muettes ? Pourtant, ici ces deux variables sont liées. J'ai un peu du mal à saisir. :cry:

par **egan** » 26 Aoû 2009, 09:16

Personne ?

par **Ericovitchi** » 26 Aoû 2009, 11:16

Oui les variables sont muettes et si tu as démontré

c'est pareil que

par **Nightmare** » 26 Aoû 2009, 12:11

struett a écrit:Bonjour à tous,

Je vais peut-être dire une énormité, mais... Si f est intégrable, elle est continue, nan? Il me semble qu'on définit l'intégrale que pour des fonctions continues...

Sur un compact, les fonction intégrables sont "presque" continues !

par **Nightmare** » 26 Aoû 2009, 12:12

(pourvu qu'elles soient bornées)

par **egan** » 26 Aoû 2009, 19:35

Quand on écrit

c'est la même chose que

?

Intégrale et fonction paire ou impaire

intégrale et fonction paire ou impaire

Qui est en ligne