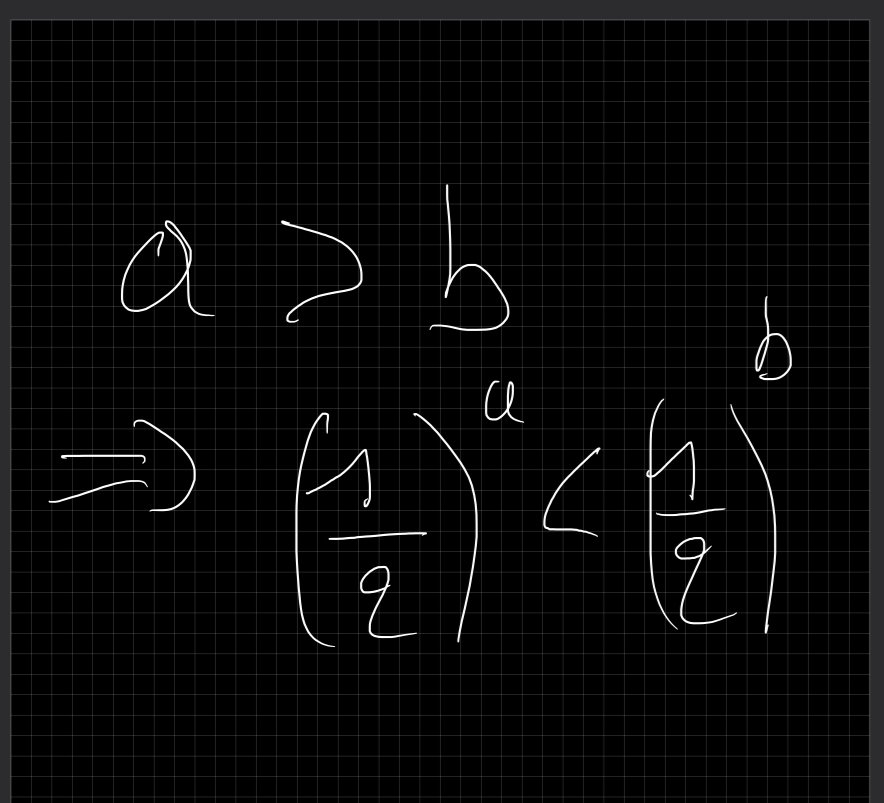Inéquations valeurs absolues

[nythostyle]

Hello, de nouveau moi je suis face à un énoncé que j'ai du mal à interpréter, mon approche de base c'est de remarquer |f(x)| > |f(x)+a| avec a >= 0, ce qui me paraît être complétement faux, je développe pour m'en assurer. f(x) > f(x)+a ou f(x) < -(f(x) +a) . Qu'est-ce que je n'ai encore pas compris dans cet énoncé svp ...

[vam]

Bonsoir

on va commencer par casser ton idée
|-4| > |-4+1| car 4>3, donc c'est possible !

Quand j'ai lu l'inéquation à résoudre, effectivement, me suis dit, la méthode la plus efficace c'est de comparer les carrés
effectivement, tu as le droit
car tu sais que si leurs carrés sont rangés dans le même ordre car la fonction carré est strictement croissante sur R+

donc oui, résous l'inégalité proposée en comparant les carrés. N'oublie pas que tu cherches x, et que a est un paramètre.

[Pisigma]

Bonjour,

tu peux écrire , de la forme

[nythostyle]

Si je suis bien le raisonnement qu'il y'a derrière, on va utiliser la méthode de comparaison des carrés car a²-b² = (a+b) * (a-b) ainsi on aura couvert l'ensemble des solutions en fonction du signe des deux membres?

[Pisigma]

oui sans oublier les contraintes sur a

[vam]

L'idée est que si tu gardes l'inégalité avec les valeurs absolues, tu vas devoir discuter tous les cas possibles pour supprimer ces valeurs absolues
alors qu'en utilisant le fait que , comme les valeurs absolues sont deux quantités positives, tu compares les carrés des valeurs absolues et tu n'as plus de valeurs absolues
Ensuite effectivement tu mets tout dans un même membre et tu utilises l'identité remarquable, cela ira plus vite pour résoudre et discuter.

[nythostyle]

Merci vam ! Puisque je suis toujours dans les inéquations j ai un peu de mal à situer l étape encadrée, pourquoi a t on changé le sens de l inégalité? La raison serait que la base du log est comprise entre 0 et 1 mais j ai du mal à voir comment ça se traduit

[nythostyle]

Serait-ce ce qui justifie le changement de sens ?

[vam]

Pour ton avant dernière réponse, le log en base 1/2 est une fonction décroissante donc
pour

Pour ta dernière réponse qu'il faudrait justifier : si alors donc

mais

[Pisigma]

en tenant compte de , on peut écrire

[nythostyle]

Merci à vous deux encore une fois