Inéquations avec valeurs absolues

[Gagnantdu06]

Bonjour,je suis bloqué à la première question de mon exercice car je ne suis pâs sur de ma réponse donc pour les autres cela pose problème:

Résolvez dans chacune des inéquations suivantes :

1) a] |x-2| 1 J'ai trouvé S = ]-;2[U]4;+[



Merci de votre aide.

[oscar]

bjr

le 1 est juste

[Gagnantdu06]

Ok merci,
le 2) est faux?

[Gagnantdu06]

EUh.. Help?

[bombastus]

Le deuxième est faux, comment as-tu fait?

[Gagnantdu06]

ben en j'ai fait une droite ou j'ai mi 3 puis j'ai soustrai 1 et additionner 1 pour trouver <1 ainsi les réels allant de [2;4] sont solutions

[bombastus]

Ah, ok, alors le premier, c'était un coup de bol...

Je recommence avec le 1)
pour résoudre |x-2| < 3, il faut différencier les cas ou x-2>0 et x-2<0
car
si x-2>0, c'est à dire x>2 alors |x-2| = ....
il faut donc résoudre
.....<3
sachant que x>2

si x-2<0, c'est à dire x<2 alors |x-2| = ....
il faut donc résoudre
.....<3
sachant que x<2

[Gagnantdu06]

Ah ok, je n'y étais pas du tout xd merci on l'a jamais fait aussi et d'un coup la prof nous sort ça.

Si x-2>0 c'est à dire x>2 alors |x-2| = x-2
il faut donc résoudre x-2<3 : x<5

Si x-2<0 c'est à dire x<2 alors |x-2| = 2-x
il faut donc résoudre 2-x<3 : -x<1 : x>-1

Mais je comprends pas comment noter S = après peux-tu m'expliquer ?

[bombastus]

Ah ok, je n'y étais pas du tout xd merci on l'a jamais fait aussi et d'un coup la prof nous sort ça.

Si x-2>0 c'est à dire x>2 alors |x-2| = x-2
il faut donc résoudre x-2[/COLOR]-1

Attention à la dernière ligne, si on multiplie par -1, il faut changer le signe de l'inéquation!

[bombastus]

S dépend des 2 ensembles que tu as trouvé

[Gagnantdu06]

Je crois avoir compris alors par exemple pour le 2) a] |3+x|1

Si 3+x>0 c'est à dire 3>x alors |3+x| = 3+x
3+x1 alors x-2

Si 3+x-3 alors |3+x| = x-3
x-31 alors x 4

On fait la réunion des deux x et on trouve
S = [-2;4] c'est cela?

[bombastus]

Je crois avoir compris alors par exemple pour le 2) a] |3+x|1

Si 3+x>0 c'est à dire 3>x alors |3+x| = 3+x
3+x1 alors x-2

Si 3+x-3 alors |3+x| = -x-3

Tu as oublié un -

[Gagnantdu06]

Ah ui! Donc S = [-4;-2] c'est cela?

[bombastus]

C'est juste!

[Gagnantdu06]

Pour voir si j'ai bien compris j'essais le suivant:
2) b] |3+x|>1

Si 3+x>0 3>x alors |3+x| = 3+x
ainsi 3+x>1 donc x>-2

Si 3+x-3 alors |3+x| = -x-3
ainsi -x-3>1 donc x<-4

Donc S = ]- ;-4[U]-2;+ [

[bombastus]

Pour voir si j'ai bien compris j'essais le suivant:
2) b] |3+x|>1

Si 3+x>0 x>-3 alors |3+x| = 3+x
ainsi 3+x>1 donc x>-2

Si 3+x1 donc x<-4

Donc S = ]- ;-4[U]-2;+ [

C'est juste mis à part ce que j'ai mis en rouge (même correction pour le 2)a)

[Gagnantdu06]

Merci à toi.
Par contre je bloque toujours au 3

[bombastus]

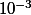
est juste un nombre tout comme 2, ou 5 sont des nombres... le principe est le même qu'avant

[Gagnantdu06]

ok Merci ......

[Gagnantdu06]

Je m'en sors pas avec ces valeurs absolues xd