Gépmétrie dans l'espace

[Flucked]

Bonjour a tous



Je n'arrive pas a faire cet exercice.

Pour la a) j'ai réussi a montrer que en effet BK=-SB+1/3SD
Pour la deuxieme partie je ne sais pas quelle chemin prendre.

merci

[Lostounet]

Hello,

Pour montrer que B, J et K sont alignés, une méthode parmi d'autres: prouver que BK et BJ sont deux vecteurs colinéaires, c'est à dire qu'on peut montrer qu'il existe un nombre tel que BK = nombreBJ

Pour trouver ce nombre, tu peux utiliser les deux expressions de BJ et BK que tu as déjà.
BJ = 3/4 SB + 1/4 SD
BK = -SB + 1/3 SD

Peux-tu trouver un nombre C tel que BJ = cBK ?

[Flucked]

Ca j'ai réussi je prends c=-3/4

Mais je n'ai pas réussi a montrer que BJ = 3/4 SB + 1/4 SD

Merci

[Lostounet]

Je pense qu'il y a une erreur dans ton énoncé, sauf erreur de ma part je trouve:

BJ = BS + SD - 1/2SD - 1/2BS + 1/4BS - 1/4SD
= BS(1 - 1/2+1/4) + SD(1 - 1/2 - 1/4)
= -3/4SB + 1/4SD

De telle sorte que: 4/3BJ = -SB + 1/3SD = BK

Voici comment j'ai procédé:
BJ = BS + SD + DO + OJ (relation de Chasles)

Sachant que:
DO = 1/2DB = 1/2(DS + SB)

Et on sait que OJ = -SJ
Sachant que 4SJ = SB + SD (par la règle du parallélogramme)

Cela totalise donc:

BJ = BS + SD + 1/2DS + 1/2SB - 1/4SB - 1/4SD

=...

[zygomatique]

salut



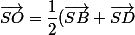or O est milieu du segment [BD] <=> (règle du parallélogramme)

[Pseuda]

Bonjour,

c) Indication :
Trouve sur la figure un point commun aux plans (SAD) et (BJC).
Quelle est la droite d'intersection de ces 2 plans ? (elle est parallèle aux plans)
Montre que cette droite est orthogonale à (SF).

[Flucked]

J'ai oublié de préciser quelque chose ...Désolé

C'est un vrai / faux donc il n'y a pas d'erreur mais simplement il faut répondre faux à la première.

Je réfléchis a tout ce que vous avez écrit. Merci pour votre aide.

[Pseuda]

Ah je suis partie de l'hypothèse que B, K et J étaient alignés. Donc tout ce que j'ai écrit ne tient pas ou presque : il faut te passer d'un point commun aux plans et montrer que les 2 plans se coupent selon une droite // (BC) et (AD) qui sont orthogonales à (SF).

d) Forme l'équation paramétrique de la droite (KJ) et calcule les coordonnées du point d'intersection de cette droite avec le plan P.

[zygomatique]

les droites (BJ) et (CJ) coupent respectivement les droites (SD) et (SA) en P et Q

la droite (PQ) est parallèle à la droite (BC) elle-même orthogonale à la droite (SF) ...

[Lostounet]

J'ai oublié de préciser quelque chose ...Désolé

C'est un vrai / faux donc il n'y a pas d'erreur mais simplement il faut répondre faux à la première.

Je réfléchis a tout ce que vous avez écrit. Merci pour votre aide.

Dans ce cas, la a) est fausse et la b) est vraie.
De toute manière elles sont incompatibles: il manque un signe - dans l'expression de BJ pour que tu puisses multiplier par 4/3

[Flucked]

Merci pour tout.

Pour la d)
B(1;0;0)
J(0;0;1)
BJ (-1;0;-1)

Equation paramétrique:
x=-t
y=0
z=1-t

En remplaçant dans l'equation du plan j'obtiens t=3 puis en revenant au système précédent je trouve x=-3 ce qui est incompatible avec la proposition donc d est fausse.

Vous etes d'accord ?

[siger]

bonjour

tout est en vecteurs

BK = -SB + SD/3
BJ =BS + SJ = BS + SO/2= BS + (SB+SD)/4 = -3SB/4+SD/4
BJ = (3/4) BK
......


equation de BJ
BJ (1;0;-1)
d'ou
x=t
y=0
z=1-t
ce qui conduit pour l'intersection avec le plan, a
2t -1+ t + 4= 0 soit t =-1
et le point d'intersection pour t=-1
omega ( -1;0;2)

[Flucked]

Merci je mettais trompé dans BJ.

Merci à tous