Geogebra
24 messages
- Page 1 sur 2 - 1, 2
 geogebra
geogebra
Bonsoir, j'ai un dm a faire mais je ne comprends rien du tout à cet exercice est ce que vous pourriez m'aidez svp?
soit P la parabole d'équation y=x² et la droite D d'équation y=mx+m, où m est un réel.
1)a)Avec le logiciel géogebra, créer un curseur m, variant de -10 à 10 avec un incrément de 0,1. Puis conjecturer la droite D et la parabole P
b)Conjecturer suivant les valeurs du réel m, l'existence du nombre de points d'intersection entre D et P, ainsi que la position relative de ces deux courbes
2) Démontrer les conjectures
soit P la parabole d'équation y=x² et la droite D d'équation y=mx+m, où m est un réel.
1)a)Avec le logiciel géogebra, créer un curseur m, variant de -10 à 10 avec un incrément de 0,1. Puis conjecturer la droite D et la parabole P
b)Conjecturer suivant les valeurs du réel m, l'existence du nombre de points d'intersection entre D et P, ainsi que la position relative de ces deux courbes
2) Démontrer les conjectures
Re: jsp
Bonjour
Cet exercice est en rapport avec ce que vous avez vu en cours à propos de l'équation d'une tangente à la courbe d'une fonction au point
au point 
Ici on sait (on le sait car l'équation de cette parabole le permet comme vous pouvez le constater algébriquement ci-dessous ) que le domaine de définition de est
est 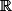 de sorte que
de sorte que 
Dans un premier temps il faudrait écrire cette tangente
=x^2) est cette fonction et donc on voit bien que son domaine de définition est l'ensemble des réels (i.e. il n'existe pas de réel qui ne possède pas d'image par cette fonction)
est cette fonction et donc on voit bien que son domaine de définition est l'ensemble des réels (i.e. il n'existe pas de réel qui ne possède pas d'image par cette fonction)
et=2x) la dérivée de cette fonction
la dérivée de cette fonction
 est cette tangente
est cette tangente
En cours vous avez vu comment calculer cette tangente
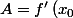) et
et 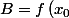-x_0 \times f^{\prime }\left(x_0\right))
À partir de là :
On commence par se rappeler comment écrire les parallèles des droites dont on connait l'équation cartésiennes
Toute parallèle de D s'écrit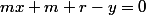 avec
avec 
Par ailleurs dans ce contexte toute perpendiculaire à cette droite s'écrira

car en cours vous avez vu que dans ce contexte le produit des deux coefficients sur des deux droites perpendiculaires est
des deux droites perpendiculaires est 
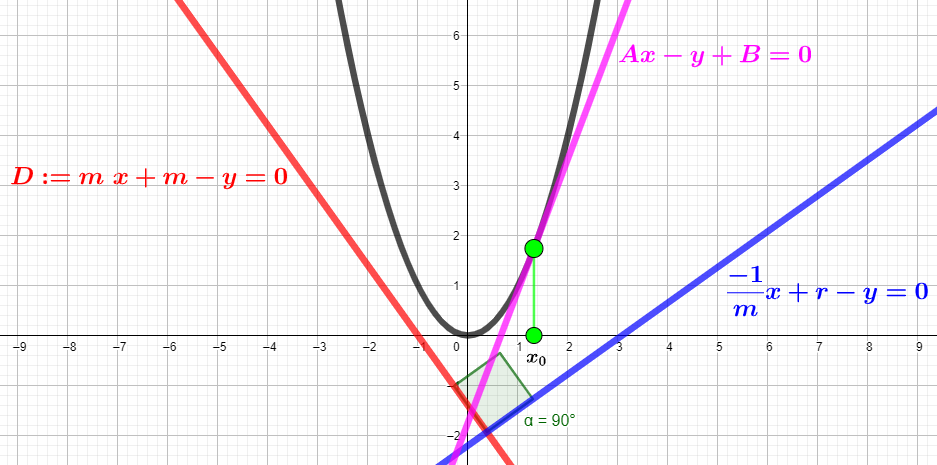
À partir de là on peut commencer à dire des choses mais jusque là êtes vous ok?
Cet exercice est en rapport avec ce que vous avez vu en cours à propos de l'équation d'une tangente à la courbe d'une fonction
Ici on sait (on le sait car l'équation de cette parabole le permet comme vous pouvez le constater algébriquement ci-dessous ) que le domaine de définition de
Dans un premier temps il faudrait écrire cette tangente
et
En cours vous avez vu comment calculer cette tangente
À partir de là :
On commence par se rappeler comment écrire les parallèles des droites dont on connait l'équation cartésiennes
Toute parallèle de D s'écrit
Par ailleurs dans ce contexte toute perpendiculaire à cette droite s'écrira
car en cours vous avez vu que dans ce contexte le produit des deux coefficients sur

À partir de là on peut commencer à dire des choses mais jusque là êtes vous ok?
Re: geogebra
strugglingwithmaths a écrit:oui pour l'instant ça va
ok donc si vous savez répondre à la question suivante et compte tenu de tout ce que j'ai dit précédemment alors vous saurez faire le reste
comment savoir si ce point est situé
-à l'intérieur de la parabole (la région du plan borné par la parabole et où se trouve son foyer)
-sur cette parabole
-à l'extérieur
Je vous laisse répondre
Re: geogebra
Regardez (la réponse à toute question se trouve toujours dans la question pour autant qu'elle soit bien posée et ça marche pour toutes les questions comme celle du genre : comment aller sur Andromède en moins de cent millions d'années mais en plus de dix minutes quand même)
L'équation de la parabole est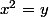 donc c'est aussi
donc c'est aussi 
Que se passe t'il si le point de coordonnées (x,y) est tel que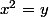 ?
?
Que se passe t-il si le point de coordonnées (x,y) est tel que ?
?
Que se passe t-il si le point de coordonnées (x,y) est tel que ?
?
C'est très important de répondre à cette question (quitte pour vous à passer plusieurs jours dessus avant d'attaquer votre exercice )
L'équation de la parabole est
Que se passe t'il si le point de coordonnées (x,y) est tel que
Que se passe t-il si le point de coordonnées (x,y) est tel que
Que se passe t-il si le point de coordonnées (x,y) est tel que
C'est très important de répondre à cette question (quitte pour vous à passer plusieurs jours dessus avant d'attaquer votre exercice )
Re: geogebra
La deuxième et dernière question que je vous pose et qui va permettre d'attaquer l'exercice est en rapport avec les équations du second degré (on ne vous aurait jamais demandé de faire cet exercice si vous n'aviez pas vu ces équations avant cela )
2)Combien de points maximum seront l'intersection de la droite D et la parabole ?
3)Comment savoir si la droite D intersecte la parabole?
Là encore regardez l'équation de la parabole (vous reconnaissez là que c'est une fonction du second degré et que les racine de vont êtres très très utiles pour répondre à ces questions) et compte tenu de la question précédente que je vous ai posé et compte tenu de l'équation de la droite alors en réfléchissant vous devriez trouver
vont êtres très très utiles pour répondre à ces questions) et compte tenu de la question précédente que je vous ai posé et compte tenu de l'équation de la droite alors en réfléchissant vous devriez trouver
2)Combien de points maximum seront l'intersection de la droite D et la parabole ?
3)Comment savoir si la droite D intersecte la parabole?
Là encore regardez l'équation de la parabole (vous reconnaissez là que c'est une fonction du second degré et que les racine de
Re: geogebra
il y a deux points d'intersections maximum.
après on fait y=y
x²=mx+m
x²-mx-m=0 après on calcule delta et apres on fait delta=0 pour trouver la valeur de m
après on fait y=y
x²=mx+m
x²-mx-m=0 après on calcule delta et apres on fait delta=0 pour trouver la valeur de m
Re: geogebra
(maximum deux et minimum zéro intersections le cas du delta négatif)
Sinon à part ça je vois que vous exploitez bien tout ce qu'il faut exploiter de votre cours
À présent on peut y aller
Sinon à part ça je vois que vous exploitez bien tout ce qu'il faut exploiter de votre cours
À présent on peut y aller
Re: geogebra
Bonjour
Cela dépend
Si vous devez rendre le fichier Geogebra il serait bon de commencer par là.
Sinon vous pouvez faire le 3° directement est ensuite répondre au 2° d'après les résultats trouvés au 3°,
Ok ce n'est pas l'ordre attendu mais bon si c'est juste pas de soucis, par contre s'il y a une erreur de calcul là cela fera mauvais effet..., donc pourquoi pas faire la figure Geogebra comme demandé dans l'énoncé ne serait ce que pour apprendre à le manipuler et s'assurer que les calculs du 3° sont justes..
Cela dépend
Si vous devez rendre le fichier Geogebra il serait bon de commencer par là.
Sinon vous pouvez faire le 3° directement est ensuite répondre au 2° d'après les résultats trouvés au 3°,
Ok ce n'est pas l'ordre attendu mais bon si c'est juste pas de soucis, par contre s'il y a une erreur de calcul là cela fera mauvais effet..., donc pourquoi pas faire la figure Geogebra comme demandé dans l'énoncé ne serait ce que pour apprendre à le manipuler et s'assurer que les calculs du 3° sont justes..
Re: geogebra
Je ne penses pas devoir rendre le fichier geogebra mais dans tous le cas je n'arrive pas vraiment à faire la figure car je n'ai jamais utilisé géogebra
Re: geogebra
Ok
je fais au plus simple
Aller sur : https://www.geogebra.org/calculator
Dans la partie gauche (là où il y a input) taper
m (Entrée)
Cela crée le paramètre m qui par défaut vaut 1 et varie de -5 à5
Sur la ligne suivante, taper :
y=x² (Entrée)
cela crée la parabole
Enfin sur la ligne suivante, taper :
y=mx+m (Entrée)
cela crée la droite
Utiliser le petit triangle play du paramètre m pour le faire varier et mettre sur pause de temps en temps.
je fais au plus simple
Aller sur : https://www.geogebra.org/calculator
Dans la partie gauche (là où il y a input) taper
m (Entrée)
Cela crée le paramètre m qui par défaut vaut 1 et varie de -5 à5
Sur la ligne suivante, taper :
y=x² (Entrée)
cela crée la parabole
Enfin sur la ligne suivante, taper :
y=mx+m (Entrée)
cela crée la droite
Utiliser le petit triangle play du paramètre m pour le faire varier et mettre sur pause de temps en temps.
Re: geogebra
pour conjecturer est ce que je dis que lorsque m=0 il semble y avoir point d'intersection et que la droite est tangente à l'hyperbole ?
Re: geogebra
oui mais il y a aussi une autre valeur (strictement négative), que tu as du trouver avec le calcul du 3eme
Re: geogebra
ah oui je me suis trompé mais je trouves pas d'autres conjectures a part pour m=0 1 point d'intersection
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 92 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
