Formes trigo et exp d'un nombre complexe

[poulou]

Bonjour à tous, Bonne année

J'aimerai juste savoir si ce que je fais est bon!!
Énoncer: Déterminer dans chaque cas le module et un argument du nombre complexe z

z=3 :

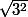
* module: = 3
* Argument: =

z=-2

*module: = -2
*argument: TEX]\frac{1}{|z|}[/TEX] =

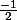
z=2i

*module: = 4
*argument: a=0 et b<0 donc Phi =

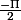
Le problème aussi c'est que je sais pas trop ce que je fais (je me suis aider d'internet pour le faire) mais je sais pas trop ce que je fais
Si vous pouviez m'expliquer
Merci à vous

[Mortelune]

Bonsoir.
Les modules sont bons pour l'argument par contre tu me perds complètement je ne vois même pas quelle formule tu utilises au début, ils sont tous faux.

edit : ah oui Low geek :dodo:

[poulou]

Pour les modules en fait, j'ai compris mais les arguments, je ne sais pas du tout comment faire. Je ne vois comprend même pas ce que c'est.

[low geek]

hello :)

il y a des erreurs la dedans tout d'abord.
z=3 le module est juste mais pas l'argument.
z=-2: les deux sont faux
z=2i pareil

z est toujours sous la forme z=x+iy tu dois le savoir :)
pour le module tu as vu juste : c'est racine de (x²+y²)
donc c'est toujours positif ;)

l'argument (on va le noté "a") a pour valeur:
cos(a)=x/|z|
sin(a)=y/|z|

dans le 1:
le module est bon et l'argument vaut:
cos(a)=3/3=1
sin(a)=0/3=0
quel est l'angle pour lequel le cosinus vaut 1 et le sinus 0 dans un cercle trigonométrique? (réponse: 0)

je te laisse appliqué tout ça pour les autres cas, si tu n'y arrive toujours pas je suis la ;)

voila tu n'a plus qu'a appliqué aux autres cas;)

[poulou]

z=-2

*Module = 2 (étourderie)
*Argument:
cos(a)= 2/-2=-1
sin (a)= 0/-2 = 0

z= 2i

*Module = =
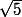
*Argument =
cos(a)= 2/
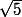
sin(a)=1/

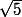
[poulou]

Petite erreur à modifier, C'est sur 2 mes arguments pour z=-2

[low geek]

dans le dernier il ne faut pas mettre "+1²" dans la racine car ici x=0

je pense après qu'avec les cos et sin tu trouve les angles facilement^^

[poulou]

dans le dernier il ne faut pas mettre "+1²" dans la racine car ici x=0

je pense après qu'avec les cos et sin tu trouve les angles facilement^^

???? Mon x= 2 et y = 1 car il ya a 1xi non??

[Sylviel]

Non tu es dans les choux : ton complexe c'est z = x + i y. Ici tu as 2i = 0 + i 2
donc x = 0, et y = 2.


Pour te répondre rapidement :
l'argument de z est l'angle entre le vecteur OM et le vecteur i des absisses. (où M est d'affixe z bien sûr). C'est pour ça qu'il est définit à 2pi près...

pour l'identifier il faut écrire :
cos a = Re(z)/|z|
sin a = Im(z)/|z|

et trouver le a qui va bien. Mais tu peux aussi "voir" l'argument directement (en particulier dans tes cas).

Attention : le module est la distance entre O et M, donc toujours positive...

Conseil : pour les complexes essaie toujours de bien suivre l'interprétation géométrique que ton prof fait lors des exercices et du cours, cela aide beaucoup...