Salut,
bon, déjà, pour ne rien te cacher, j'ai été intrigué par le titre "3 formes pour les complexes" (je me suis dit que j'en connais bien 3, mais la troisième, à savoir les matrices n'est pas pas vue au lycée).
Donc je regarde, et là, je comprend mieux...
Donc je commencerais par dire que, pour moi, entre la "forme trigo" et "la forme exponentielle", c'est "blanc bonnet et bonnet blanc" c'est juste deux façons différentes d'écrire exactement la même chose, vu que
par définition (à ton niveau)
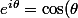+i\sin(\theta)\)
Aprés, je t'avoue que le "pourquoi" de la question me laisse un peu perplexe : on pourrait parfaitement inventer des tonnes d'autres formes (moins pratiques pour les calculs fait au lycée) pour écrire les complexes.
Par contre je pense qu'une question pertinente serait plutôt "à quoi servent les deux formes des nombres complexes vues au Lycée" et là, je pense que la réponse qui s'impose (niveau Lycée) est :
- La forme cartésienne permet trés simplement de faire des additions/soustraction, mais c'est merdique (mais faisable quand même) pour les multilications/divisions et racines carrées (avec un s)
- La forme polaire permet trés simplement de faire des multiplications/divisions et de trouver les racines n-ièmes mais est quasi inutile pour les additions/soustractions.
