Fonctions
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
JuliaKori
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2015, 13:01
-
 par JuliaKori » 14 Nov 2015, 13:32
par JuliaKori » 14 Nov 2015, 13:32
-
JuliaKori
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2015, 13:01
-
 par JuliaKori » 14 Nov 2015, 13:36
par JuliaKori » 14 Nov 2015, 13:36
Excusez-moi pour la question
4)a), c'est non ,

mais

:lol3:

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 14 Nov 2015, 13:37
par Lostounet » 14 Nov 2015, 13:37
Salut,
As-tu essayé une récurrence pour le 4)a ) ? :)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
biss
- Membre Rationnel
- Messages: 659
- Enregistré le: 30 Oct 2015, 18:02
-
 par biss » 14 Nov 2015, 14:20
par biss » 14 Nov 2015, 14:20
ici je ne vois rien qui concerne Un et c'est quoi le ? dans Vn[?]
-
JuliaKori
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2015, 13:01
-
 par JuliaKori » 14 Nov 2015, 15:12
par JuliaKori » 14 Nov 2015, 15:12
biss a écrit:ici je ne vois rien qui concerne Un et c'est quoi le ? dans Vn[?]
c'est un carré (²)
-
JuliaKori
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2015, 13:01
-
 par JuliaKori » 14 Nov 2015, 15:14
par JuliaKori » 14 Nov 2015, 15:14
biss a écrit:ici je ne vois rien qui concerne Un et c'est quoi le ? dans Vn[?]
J'ai corrigé pour le Un, voir mon message précédent :lol3:
-
JuliaKori
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2015, 13:01
-
 par JuliaKori » 14 Nov 2015, 15:16
par JuliaKori » 14 Nov 2015, 15:16
Lostounet a écrit:Salut,
As-tu essayé une récurrence pour le 4)a ) ?

Justement , je sais qu'on peut faire une récurrence mais je ne sais pas comment raisonner :mur:
Je fais :
Initialisation : v0=a
et 4*(a/4)^2^0 = 4*(a/4)=a donc p(0) est vraie
et après ?

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 14 Nov 2015, 15:22
par Lostounet » 14 Nov 2015, 15:22
Tu supposes Vn = 4*(a/4)^(2^n)
f(Vn) = (4*(a/4)^(2^n))^2/4 = 4*((a/4)^(2^n)^2) = 4*((a/4)^(2^n+1) = Vn+1
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
biss
- Membre Rationnel
- Messages: 659
- Enregistré le: 30 Oct 2015, 18:02
-
 par biss » 14 Nov 2015, 15:24
par biss » 14 Nov 2015, 15:24
suppose que Vn est vrai
si Vn est vrai alors (Vn[2])/4 =Vn+1 et tu as ta reponse
-
JuliaKori
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2015, 13:01
-
 par JuliaKori » 14 Nov 2015, 16:31
par JuliaKori » 14 Nov 2015, 16:31
Je ne comprends pas, dans 4*((a/4)^(2^n)^2) , pourquoi le /4 disparaît :hein:
-
JuliaKori
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2015, 13:01
-
 par JuliaKori » 14 Nov 2015, 16:35
par JuliaKori » 14 Nov 2015, 16:35
Lostounet a écrit:Tu supposes Vn = 4*(a/4)^(2^n)
f(Vn) = (4*(a/4)^(2^n))^2/4 = 4*((a/4)^(2^n)^2) = 4*((a/4)^(2^n+1) = Vn+1
Pourriez-vous m'expliquer juste comment vous passer de l'étape 1 à 2 svp :happy2:

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 14 Nov 2015, 16:47
par Lostounet » 14 Nov 2015, 16:47
(p^n)^m = p^(n*m)
((a/4)^(2^n))^2 = (a/4)^(2^n *2) = (a/4)^(2^(n + 1))
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
JuliaKori
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2015, 13:01
-
 par JuliaKori » 14 Nov 2015, 16:51
par JuliaKori » 14 Nov 2015, 16:51
Lostounet a écrit:(p^n)^m = p^(n*m)
((a/4)^(2^n))^2 = (a/4)^(2^n *2) = (a/4)^(2^(n + 1))
Merci :lol3:
-
JuliaKori
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2015, 13:01
-
 par JuliaKori » 14 Nov 2015, 16:55
par JuliaKori » 14 Nov 2015, 16:55
JuliaKori a écrit:Pourriez-vous m'expliquer juste comment vous passer de l'étape 1 à 2 svp :happy2:
Il n'y a que ça que je ne comprends pas

-
JuliaKori
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2015, 13:01
-
 par JuliaKori » 14 Nov 2015, 18:08
par JuliaKori » 14 Nov 2015, 18:08

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 14 Nov 2015, 18:11
par Lostounet » 14 Nov 2015, 18:11
Mais on vient de le faire... on a montré que P(n) => P(n + 1) et P(0) vraie...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
JuliaKori
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2015, 13:01
-
 par JuliaKori » 14 Nov 2015, 18:13
par JuliaKori » 14 Nov 2015, 18:13
Oui mais dans mon raisonnement , je fais

=)
^{(2_{n})})^2}{4})
= ?
Vous m'avez fais le raisonnement dans les messages précédents mais je ne l'ai pas compris, du moins pas tout ...
-
JuliaKori
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2015, 13:01
-
 par JuliaKori » 14 Nov 2015, 18:14
par JuliaKori » 14 Nov 2015, 18:14
Comment supprimer le dénominateur 4 dans la fraction ?

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 14 Nov 2015, 18:15
par Lostounet » 14 Nov 2015, 18:15
En fait c'est faux: C'est V_n+1 qui vaut f(V_n) !
En supposant que Vn s'écrit 4*(a/4)^(2^n) pour n donné, on veut montrer que Vn+1 s'écrit alors 4*(a/4)^(2^(n + 1))).
Et pour passer de Vn à Vn+1, j'applique f !
Refais le calcul et tu verras pour le /4
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
JuliaKori
- Membre Naturel
- Messages: 36
- Enregistré le: 19 Sep 2015, 13:01
-
 par JuliaKori » 14 Nov 2015, 18:18
par JuliaKori » 14 Nov 2015, 18:18
Lostounet a écrit:
Et pour passer de Vn à Vn+1, j'applique f !
Refais le calcul et tu verras pour le /4
Oui je sais :we: J'ai bien compris le principe de la récurrence c'est juste que je ne sais pas faire le calcul pour arriver jusqu'à Vn+1 ...
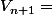
=)
^{(2_{n})})^2}{4})
=...=

C'est les "..." que je n'arrive pas à faire :lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
