Fonction rationnelle. Comment trouver les 2 points les plus rapprochés?
33 messages
- Page 1 sur 2 - 1, 2
Fonction rationnelle. Comment trouver les 2 points les plus rapprochés?
Bonsoir à tous,
Je suis tout nouveau sur votre forum, et déjà, j'ai une question pour vous...
Je suis présentement face à un problème qui me demande, formulé dans une belle mise en situation, quelle est la distance minimale entre les 2 courbes que forme la fonction rationnelle
f(x)=y=((1600/(x-20))+1000
J'ai cherché en vain à résoudre ce problème, et la meilleure façon d'y arriver que j'ai trouvé est de trouver les coordonnées du point central de chacune des courbes puis d'appliquer la formule de la distance entre 2 points.
Seulement, j'ignore comment trouver les coordonnées de ces points, ni même si c'est possible...
Merci de bien vouloir me donner un coup de main
Je suis tout nouveau sur votre forum, et déjà, j'ai une question pour vous...
Je suis présentement face à un problème qui me demande, formulé dans une belle mise en situation, quelle est la distance minimale entre les 2 courbes que forme la fonction rationnelle
f(x)=y=((1600/(x-20))+1000
J'ai cherché en vain à résoudre ce problème, et la meilleure façon d'y arriver que j'ai trouvé est de trouver les coordonnées du point central de chacune des courbes puis d'appliquer la formule de la distance entre 2 points.
Seulement, j'ignore comment trouver les coordonnées de ces points, ni même si c'est possible...
Merci de bien vouloir me donner un coup de main
Merci d'avoir répondu si rapidement,
Pour ce qui est de savoir si cela forme 1 courbe ou 2, j'ai appris que les fonction rationnelle (La fonction rationnelle de base étant y=1/x) donne 2 courbes symétriques et opposées...
Dans le cas de la fonction de base y=1/x,
Nous aurons 2 courbes opposées par le point d'origine qui s'approcheront indéfiniment des axes x et y sans jamais les toucher....
Voici une image...

Théoriquement cette fonction ne définit qu'une courbe mais bon, sur graphique on en voit 2.
Pour ce qui est de savoir si cela forme 1 courbe ou 2, j'ai appris que les fonction rationnelle (La fonction rationnelle de base étant y=1/x) donne 2 courbes symétriques et opposées...
Dans le cas de la fonction de base y=1/x,
Nous aurons 2 courbes opposées par le point d'origine qui s'approcheront indéfiniment des axes x et y sans jamais les toucher....
Voici une image...

Théoriquement cette fonction ne définit qu'une courbe mais bon, sur graphique on en voit 2.
ok, merci pour les précisions.
Au fait, je suppose que tu es au lycée (1ere ou Tale), je vois mal comment on pourrait étudier ça au collège (enfin, ce qu'on appelle lycée en France, tu es au Québec, c'est ça ?)
Bon, je pense que le point "central" est celui où la dérivée vaut -1 (la tangente a un angle de 45 degrés), il faudrait donc calculer la dérivée et trouver ces deux points.
Au fait, je suppose que tu es au lycée (1ere ou Tale), je vois mal comment on pourrait étudier ça au collège (enfin, ce qu'on appelle lycée en France, tu es au Québec, c'est ça ?)
Bon, je pense que le point "central" est celui où la dérivée vaut -1 (la tangente a un angle de 45 degrés), il faudrait donc calculer la dérivée et trouver ces deux points.
Merci encore pour ton aide,
Oui je suis du Québec (secondaire 5, mathématique 536). Désolé d'avoir posté dans la mauvaise section, je ne savais pas trop vers où me diriger)
Donc, déjà avant d'essayer ce que tu me propose, j'ai un autre problème...
Il y a des termes dans ton explications qui me sont complètement inconnus.
Dont le plus importants...dérivée. Je n'ai jamais entendu ce terme, tu crois que tu pourrais me donner un petit cours sur les expressions mathématiques française ?
Oui je suis du Québec (secondaire 5, mathématique 536). Désolé d'avoir posté dans la mauvaise section, je ne savais pas trop vers où me diriger)
Donc, déjà avant d'essayer ce que tu me propose, j'ai un autre problème...
Il y a des termes dans ton explications qui me sont complètement inconnus.
Dont le plus importants...dérivée. Je n'ai jamais entendu ce terme, tu crois que tu pourrais me donner un petit cours sur les expressions mathématiques française ?
Fraggs a écrit:Merci encore pour ton aide,
Oui je suis du Québec (secondaire 5, mathématique 536). Désolé d'avoir posté dans la mauvaise section, je ne savais pas trop vers où me diriger)
Donc, déjà avant d'essayer ce que tu me propose, j'ai un autre problème...
Il y a des termes dans ton explications qui me sont complètement inconnus.
Dont le plus importants...dérivée. Je n'ai jamais entendu ce terme, tu crois que tu pourrais me donner un petit cours sur les expressions mathématiques française ?
Est-ce que tu ne comprends pas le terme "dérivée" ou la notion de dérivée ???
Si c'est juste le terme, ce que nous appelons "dérivée" sont les fonctions f' issues de f qui se calculent comme ça
f'(x) pour une fonction de type
Ainsi la dérivée de
Ensuite viennent les règles des opérations sur comment dériver une fonction pouvant être vue comme la composition de deux fonctions plus simples u et v
(u+v)'=u'+v'
(uv)'=uv' + u'v
(u/v)'= (uv' - u'v)/v²
(u(v))'=u'(v) * v'
Si c'est la "notion" de dérivée que tu ne connais pas, alors cela va devenir un peu plus long à expliquer...
Bonjour,
j'ai fait un peu de recherches sur internet et il semblerait que le secondaire 5 corresponde à notre classe de 2nde: http://zonemath.csmv.qc.ca/liens/niveaux.html
J'ai aussi vérifié le programme de maths 536 et il n'y a pas de dérivées (ce qui n'est pas vraiment surprenant, vu qu'on fait ça en première chez nous)
Il faut donc résoudre sans utiliser de dérivées
j'ai fait un peu de recherches sur internet et il semblerait que le secondaire 5 corresponde à notre classe de 2nde: http://zonemath.csmv.qc.ca/liens/niveaux.html
J'ai aussi vérifié le programme de maths 536 et il n'y a pas de dérivées (ce qui n'est pas vraiment surprenant, vu qu'on fait ça en première chez nous)
Il faut donc résoudre sans utiliser de dérivées
il faire ça avec des considérations géométriques à mon avis. Prenons le cas de la fonction 1/x.
Par symétrie de la courbe, on voit que le point de la demi-courbe de droite le plus proche de la demi courbe de gauche est aussi le point le plus proche de O. Il s'agit, comme l'a dit "Fraggs", du point central, que l'on peut constrire géométriquement comme étant le point qui se trouve sur la droite y=x.
Pour trouver ce point, il faut donc égaliser x=1/x soit x=1. La distance entre (1,1) et O est donc la plus petite distance entre les deux moitiés de la courbe est
donc la plus petite distance entre les deux moitiés de la courbe est 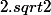
Maintenant, dans ton exercice, il faut trouver le point de symétrie de ta courbe et adapter la méthode.
Par symétrie de la courbe, on voit que le point de la demi-courbe de droite le plus proche de la demi courbe de gauche est aussi le point le plus proche de O. Il s'agit, comme l'a dit "Fraggs", du point central, que l'on peut constrire géométriquement comme étant le point qui se trouve sur la droite y=x.
Pour trouver ce point, il faut donc égaliser x=1/x soit x=1. La distance entre (1,1) et O est
Maintenant, dans ton exercice, il faut trouver le point de symétrie de ta courbe et adapter la méthode.
uztop a écrit:. Il s'agit, comme l'a dit "Fraggs", du point central, que l'on peut constrire géométriquement comme étant le point qui se trouve sur la droite y=x.
Peut-on prouver que ce point central C(1; 1) est bien le plus proche du point de symétrie (ici O) sans utiliser de dérivée ?
Géométriquement, la distance la plus courte entre un point P et une courbe C se traduit par la création d'un point M appartenant à C tel que la tangente à C en M sera perpendiculaire à PM. Alors la distance séparant P de M est la distance la plus courte possible entre P et la courbe.
Dans l'exemple y=1/x, la tangente à la courbe en C donne une droite d'équation y=-x + k et cette droite est bien perpendiculaire à la droite y=x. Pour trouver l'équation de cette tangente, je suis passé par la dérivée. Mais sans ça... :briques:
uztop a écrit:je dirais qu'en seconde, on ne peut pas le montrer de manière formelle; on peut par contre constater en traçant la droite y=x et la tangente à la courbe en C que ces deux droites sont bien perpendiculaires, ce qui montre que c'est bien le point le plus proche
Mouais. Personnellement j'aime pas les résultats donnés "au feeling" mais si c'est la seule possibilité...
Bon matin,
C'est un peu dur en se réveillant, mais je crois avoir saisis...
Donc, dans ma situation, le point de symétrie est (20,1000) soit l'endroit où se rejoignent mes 2 asymptotes. Ainsi donc je dois trouver le point dans l'une ou l'autre des courbes qui est le plus rapproché de ces coordonnés.
C'est là que je bloque encore...Je crois avoir plus ou moins compris comment tu y étais arrivé uztop, mais lorsque j'essaie avec ma situation, j'arrive à 2 réponses soit 18,37 et 1001,63. Si je me fie à ce que j'ai compris de ton explication, le point central de ma courbe serait situé soit en (18.37;18.37) ou en (1001.63;1001.63) ce qui est impossible...
Merci de votre aide.
C'est un peu dur en se réveillant, mais je crois avoir saisis...
Donc, dans ma situation, le point de symétrie est (20,1000) soit l'endroit où se rejoignent mes 2 asymptotes. Ainsi donc je dois trouver le point dans l'une ou l'autre des courbes qui est le plus rapproché de ces coordonnés.
C'est là que je bloque encore...Je crois avoir plus ou moins compris comment tu y étais arrivé uztop, mais lorsque j'essaie avec ma situation, j'arrive à 2 réponses soit 18,37 et 1001,63. Si je me fie à ce que j'ai compris de ton explication, le point central de ma courbe serait situé soit en (18.37;18.37) ou en (1001.63;1001.63) ce qui est impossible...
Merci de votre aide.
Salut,
oui, tu as utilisé une bonne méthode pour le point de symétrie et ta réponse est juste (le point de coordonnées (20;1000) )
Maintenant, il faut tracer une droite de pente 1 qui passe par ce point et voir à quel moment elle rencontre la courbe.
Les résultats que tu trouves ne sont pas bons (tu dois avoir tracé une mauvaise droite)
PS: pour le "bon matin", c'est un peu tard: il fait déjà nuit ici :)
oui, tu as utilisé une bonne méthode pour le point de symétrie et ta réponse est juste (le point de coordonnées (20;1000) )
Maintenant, il faut tracer une droite de pente 1 qui passe par ce point et voir à quel moment elle rencontre la courbe.
Les résultats que tu trouves ne sont pas bons (tu dois avoir tracé une mauvaise droite)
PS: pour le "bon matin", c'est un peu tard: il fait déjà nuit ici :)
Ah ok, j'avais mal compris alors ^^
Présentement je suis au boulot donc je ne peux essayer tout de suite, mais dès que je rentre je tente le coup.
Comme je ne peux résoudre le problème graphiquement, je veux m'assurer de ne pas partir avec de mauvaises équations de base.
Donc l'équation de ma droite sécantes aux 2 courbes sera
y=x+980 ?
Soit
y=ax+b
1000=1*20+b
1000=20+b
980=b
y=1x+980
Ensuite je n'ai qu'à trouvé les coordonnés du points ou la courbe et la droite sont sécantes...
C'est bien ça ?
Présentement je suis au boulot donc je ne peux essayer tout de suite, mais dès que je rentre je tente le coup.
Comme je ne peux résoudre le problème graphiquement, je veux m'assurer de ne pas partir avec de mauvaises équations de base.
Donc l'équation de ma droite sécantes aux 2 courbes sera
y=x+980 ?
Soit
y=ax+b
1000=1*20+b
1000=20+b
980=b
y=1x+980
Ensuite je n'ai qu'à trouvé les coordonnés du points ou la courbe et la droite sont sécantes...
C'est bien ça ?
33 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
