Fonction logarithme népérien
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
henri896
- Membre Relatif
- Messages: 122
- Enregistré le: 25 Avr 2007, 13:27
-
 par henri896 » 14 Déc 2008, 14:35
par henri896 » 14 Déc 2008, 14:35
bonjour je ne comprends pas comment faire cet exercice pouvez vous m'aider svp...
On a une fonction définie sur ]0; +infini[ par:
f(x)= 2x ln (x) -3x
a) il faut trouver sa dérivée f'(x)
puis calculer f(e) et f'(e)
en ce qui concerne f'(x) je trouve O est ce cela?
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 14 Déc 2008, 14:38
par axiome » 14 Déc 2008, 14:38
henri896 a écrit:en ce qui concerne f'(x) je trouve O est ce cela?
Tu dois avoir fait une erreur...
Tu peux détailler ton calcul ?
-
henri896
- Membre Relatif
- Messages: 122
- Enregistré le: 25 Avr 2007, 13:27
-
 par henri896 » 14 Déc 2008, 14:42
par henri896 » 14 Déc 2008, 14:42
ca me fait : 2+1-3
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 14 Déc 2008, 14:52
par axiome » 14 Déc 2008, 14:52
Ta fonction est bien :
=2xln(x)-3x)
?
Parce que ton calcul de dérivée est faux : pour dériver f, il faut que tu dérives d'abord
)
(u'*v+u*v') et ensuite
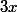
-
henri896
- Membre Relatif
- Messages: 122
- Enregistré le: 25 Avr 2007, 13:27
-
 par henri896 » 14 Déc 2008, 14:54
par henri896 » 14 Déc 2008, 14:54
oui c'est bien cette fonction
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 14 Déc 2008, 14:55
par axiome » 14 Déc 2008, 14:55
Ben, si c'est bien cette fonction, ce n'est pas 0 sa dérivée.
-
henri896
- Membre Relatif
- Messages: 122
- Enregistré le: 25 Avr 2007, 13:27
-
 par henri896 » 14 Déc 2008, 14:59
par henri896 » 14 Déc 2008, 14:59
pouvez vous me dire ce qu'est le v dans la formule parce qu'avec ln je ne sais pas le dérivé
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 14 Déc 2008, 15:01
par axiome » 14 Déc 2008, 15:01
La dérivée de ln(x) est 1/x. Je pense que ça doit être marqué dans ton cours.
-
henri896
- Membre Relatif
- Messages: 122
- Enregistré le: 25 Avr 2007, 13:27
-
 par henri896 » 14 Déc 2008, 15:02
par henri896 » 14 Déc 2008, 15:02
donc la dérivée est 2x(1/x)-3 ?
-
lnlnln
- Messages: 6
- Enregistré le: 14 Déc 2008, 14:45
-
 par lnlnln » 14 Déc 2008, 15:04
par lnlnln » 14 Déc 2008, 15:04
ba le v c lnx é normalmen tu doi conètr la dérivé de lnx
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 14 Déc 2008, 15:05
par axiome » 14 Déc 2008, 15:05
henri896 a écrit:f(x)= 2x ln (x) -3x
J'ai un doute.
Le symbole en rouge dans ta fonction, c'est un symbole fois ou une variable x ?
Parce que tu as l'air de raisonner comme s'il s'agissait du symbole fois.
Moi, je l'ai pris comme une variable x, pas comme le symbole fois.
-
henri896
- Membre Relatif
- Messages: 122
- Enregistré le: 25 Avr 2007, 13:27
-
 par henri896 » 14 Déc 2008, 15:15
par henri896 » 14 Déc 2008, 15:15
donc la dérivée est 2x(1/x)-3 ?
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 14 Déc 2008, 15:16
par axiome » 14 Déc 2008, 15:16
henri896 a écrit:donc la dérivée est 2x(1/x)-3 ?
Ca dépend du symbole en rouge marquée dont je te parle ci dessus.
Est-ce un symbole fois ou est-ce la variable x ?
-
henri896
- Membre Relatif
- Messages: 122
- Enregistré le: 25 Avr 2007, 13:27
-
 par henri896 » 14 Déc 2008, 15:17
par henri896 » 14 Déc 2008, 15:17
je dirais le x de la multiplication
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 14 Déc 2008, 15:20
par axiome » 14 Déc 2008, 15:20
henri896 a écrit:je dirais le x de la multiplication
Oki, si tu dis qu'il s'agit du x de la multiplication, la dérivée de la fonction f est en effet 2(1/x)-3.
-
henri896
- Membre Relatif
- Messages: 122
- Enregistré le: 25 Avr 2007, 13:27
-
 par henri896 » 14 Déc 2008, 15:21
par henri896 » 14 Déc 2008, 15:21
donc on peut dire que c'est égal à (2:x)-3?
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 14 Déc 2008, 15:24
par axiome » 14 Déc 2008, 15:24
henri896 a écrit:donc on peut dire que c'est égal à (2:x)-3?
ben évidemment, c'est la même chose que (2/x)-3. Perso, je mettrais sur même dénominateur le résultat.
-
henri896
- Membre Relatif
- Messages: 122
- Enregistré le: 25 Avr 2007, 13:27
-
 par henri896 » 14 Déc 2008, 15:31
par henri896 » 14 Déc 2008, 15:31
d'accord , ensuite pour f(e) j'ai trouvé : -e
puis pour f'(e) jé trouvé -1
ais-je bon?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
