Fonction, limites aux bornes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
gioser
- Membre Naturel
- Messages: 50
- Enregistré le: 23 Sep 2006, 10:41
-
 par gioser » 24 Sep 2006, 10:05
par gioser » 24 Sep 2006, 10:05
Bonjour, cette fonction m'intrigue...
Soit f la fonction définie par: f(x)=(x²-x^3)/(2x²+x-3)
Donner l'ensemble de définition de la fonction f et étudier les limites de f aux bornes de son ensemble de définition.
Quelqu'un peut-il m'éclairer? Merci. :zen:
-
nxthunder
- Membre Relatif
- Messages: 224
- Enregistré le: 30 Juin 2005, 09:16
-
 par nxthunder » 24 Sep 2006, 10:13
par nxthunder » 24 Sep 2006, 10:13
Salut,
f est définie si le dénominateur ne s'annule pas
Donc calcul le discrimant du dénominateur
Et tu obtiendras qqch du type

Ensuite tu calcules les limites en

, en

, en

, puis en

-
gioser
- Membre Naturel
- Messages: 50
- Enregistré le: 23 Sep 2006, 10:41
-
 par gioser » 24 Sep 2006, 10:31
par gioser » 24 Sep 2006, 10:31
delta= b²-4ac
delta= 1²-4X(2X-3)
delta= 1²+4X-6
delta= 1+24
delta= 25
Oui, et ensuite?
-
nxthunder
- Membre Relatif
- Messages: 224
- Enregistré le: 30 Juin 2005, 09:16
-
 par nxthunder » 24 Sep 2006, 10:39
par nxthunder » 24 Sep 2006, 10:39
Ensuite, tu calcules les racines du polynomes
Tu en déduis l'ensemble de définition et tu calcules les limites
-
gioser
- Membre Naturel
- Messages: 50
- Enregistré le: 23 Sep 2006, 10:41
-
 par gioser » 24 Sep 2006, 10:57
par gioser » 24 Sep 2006, 10:57
Donc on aura:
x=1 d'un côté, et x=-1.5 de l'autre côté.
Df: ]-oo;-1.5[U]1;+oo[
C'est bien cela?
-
nxthunder
- Membre Relatif
- Messages: 224
- Enregistré le: 30 Juin 2005, 09:16
-
 par nxthunder » 24 Sep 2006, 10:58
par nxthunder » 24 Sep 2006, 10:58
Pas tout a fait,
Elle est aussi définie entre ]-1.5 ; 1 [
-
gioser
- Membre Naturel
- Messages: 50
- Enregistré le: 23 Sep 2006, 10:41
-
 par gioser » 24 Sep 2006, 10:59
par gioser » 24 Sep 2006, 10:59
nxthunder a écrit:Pas tout a fait,
Elle est aussi définie entre ]-1.5 ; 1 [
Ah oui, pardon.
Mais dans ce cas là, combien de limites à calculer?
les bornes -oo et +oo ou bien toutes les bornes?
-
nxthunder
- Membre Relatif
- Messages: 224
- Enregistré le: 30 Juin 2005, 09:16
-
 par nxthunder » 24 Sep 2006, 11:01
par nxthunder » 24 Sep 2006, 11:01
TOutes les bornes
C'est à dire en

;

;

;
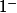
;

;

-
gioser
- Membre Naturel
- Messages: 50
- Enregistré le: 23 Sep 2006, 10:41
-
 par gioser » 24 Sep 2006, 11:05
par gioser » 24 Sep 2006, 11:05
Cela me parait compliqué... On tombe sur des FI à chaque fois il me semble...
-
nxthunder
- Membre Relatif
- Messages: 224
- Enregistré le: 30 Juin 2005, 09:16
-
 par nxthunder » 24 Sep 2006, 11:07
par nxthunder » 24 Sep 2006, 11:07
penses a mettre le terme de plus haut degré en facteur
-
gioser
- Membre Naturel
- Messages: 50
- Enregistré le: 23 Sep 2006, 10:41
-
 par gioser » 24 Sep 2006, 11:08
par gioser » 24 Sep 2006, 11:08
nxthunder a écrit:penses a mettre le terme de plus haut degré en facteur
Pour chaque limite? du type: lim f x->-oo= x^3/2x²
-
nxthunder
- Membre Relatif
- Messages: 224
- Enregistré le: 30 Juin 2005, 09:16
-
 par nxthunder » 24 Sep 2006, 11:12
par nxthunder » 24 Sep 2006, 11:12
gioser a écrit:Bonjour, cette fonction m'intrigue...
Soit f la fonction définie par:
=\frac{(x^2-x^3)}{(2x^2+x-3)})
Attention c'est pas

!!!!
Et tu as juste a mettre le terme de plus haut degre en facteur lorsque tu as a calculer les limites qui tendent vers

car la parenthese tendra vers 1.
-
gioser
- Membre Naturel
- Messages: 50
- Enregistré le: 23 Sep 2006, 10:41
-
 par gioser » 24 Sep 2006, 11:14
par gioser » 24 Sep 2006, 11:14
Merci de m'aider nxthunder, tu sais j'ai beau essayer et ré-essayer, les maths ne sont pas faites pour moi :triste:
-
gioser
- Membre Naturel
- Messages: 50
- Enregistré le: 23 Sep 2006, 10:41
-
 par gioser » 24 Sep 2006, 11:18
par gioser » 24 Sep 2006, 11:18
Pourrais-tu me donner un petit coup de pouce pour cette dernière ligne droite?
-
nxthunder
- Membre Relatif
- Messages: 224
- Enregistré le: 30 Juin 2005, 09:16
-
 par nxthunder » 24 Sep 2006, 11:33
par nxthunder » 24 Sep 2006, 11:33
Bon je te donne l'exemple avec 1 limite apres essaye de t'en inspirer

Calculons la limite de f en

)
=

Tu mets le terme de plus haut degre en facteur :
Ainsi tu vas obtenir ceci :
}{2x^2 (1+\frac{1}{2x}-\frac{3}{2x^2})})


Tu appliques la meme methode pour

et ainsi de suite pour les autres limites
-
gioser
- Membre Naturel
- Messages: 50
- Enregistré le: 23 Sep 2006, 10:41
-
 par gioser » 24 Sep 2006, 11:34
par gioser » 24 Sep 2006, 11:34
nxthunder a écrit:Bon je te donne l'exemple avec 1 limite apres essaye de t'en inspirer

Calculons la limite de f en

)
=

Tu mets le terme de plus haut degre en facteur :
Ainsi tu vas obtenir ceci :
}{2x^2 (1+\frac{1}{2x}-\frac{3}{2x^2})})


Tu appliques la meme methode pour

et ainsi de suite pour les autres limites
Ok merci ca marche
-
gioser
- Membre Naturel
- Messages: 50
- Enregistré le: 23 Sep 2006, 10:41
-
 par gioser » 24 Sep 2006, 11:44
par gioser » 24 Sep 2006, 11:44
Ca donnerait:
lim f lorsque x-> -1.5= lim x²(1-x)/ x(2x+1)= lim x(1-x)/ 2x+1= ah je ne sais pas
-
nxthunder
- Membre Relatif
- Messages: 224
- Enregistré le: 30 Juin 2005, 09:16
-
 par nxthunder » 24 Sep 2006, 11:49
par nxthunder » 24 Sep 2006, 11:49
Remplace X par -1.5 tout simplement :)
Mais attention distingues le cas ou x tend vers-1.5 a gauche et ou x tend vers -1.5 a droite
PS : ce que tu as marqué est faux
-
gioser
- Membre Naturel
- Messages: 50
- Enregistré le: 23 Sep 2006, 10:41
-
 par gioser » 24 Sep 2006, 13:20
par gioser » 24 Sep 2006, 13:20
En résumé,
limf lorsque x->-oo= +oo
limf lorsque x->-3/2= 0+
limf lorsque x->1= 0-
limf lorsque x->+oo= -oo
C'est bien cela?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
