Limites aux bornes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
LuluCooooper
- Membre Relatif
- Messages: 185
- Enregistré le: 29 Oct 2007, 18:05
-
par LuluCooooper » 04 Oct 2009, 17:08
Bonsoir !
je dois étudier g, je suis en train de faire les limites aux bornes :
= \frac{(x+3)^4+1}{(x+3)^2})
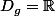
/{-3}
g peut s'écrire sous la forme
 = (x+3)^2 + \frac{1}{(x+3)^2})
 =+\infty)
 =-\infty)
Mais je fais comment quand x tend vers -3 ?? Par valeur inférieures et supérieures mais j'ai toujours 0/0
Je trouve pas comment factoriser pour avoir des bonnes limites
Merci d'avance pour votre aide
-
Laurent Porre
- Membre Relatif
- Messages: 198
- Enregistré le: 22 Juin 2007, 10:00
-
par Laurent Porre » 04 Oct 2009, 17:12
LuluCooooper a écrit:g peut s'écrire sous la forme
es-tu sur que tu as un 0/0 en -3 ??
que vaut la limite de
^2})
en -3 ?
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
par le_fabien » 04 Oct 2009, 17:14
Bonsoir,
mais non quand x tend vers -3 on a 1/0.
Edit : oups j'avais pas vu ton post Laurent...
-
LuluCooooper
- Membre Relatif
- Messages: 185
- Enregistré le: 29 Oct 2007, 18:05
-
par LuluCooooper » 04 Oct 2009, 17:30
Ok alors
^2 = 0)
Quand x-3
^2} = +\infty)
D'où
Quand x-3
 = +\infty)
C'est bon ?
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
par le_fabien » 04 Oct 2009, 17:58
LuluCooooper a écrit:Ok alors
Quand x-3
D'où
Quand x-3
C'est bon ?
Ok c'est bon. :zen:
-
LuluCooooper
- Membre Relatif
- Messages: 185
- Enregistré le: 29 Oct 2007, 18:05
-
par LuluCooooper » 04 Oct 2009, 18:14
Ok merci !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
