Bonjour,
J'ai rencontré un exercice dans lequel on demande de trouver à quelle intervalle appartient 1/x si x appartient à l'intervalle] 0;5] et du coup la réponse est [1/5 ;+ l'infini [, je ne comprends pas d'où vient le + l'infini. Pouvez zvius l'expliquer svp.
Merci d'avance pour votre aide.
Fonction inverse 2de
6 messages
- Page 1 sur 1
Re: Fonction inverse 2de
Bonjour,
Par simple décroissance de la fonction inverse sur les réels strictement positifs, on a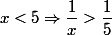 , donc l'image d'un nombre compris entre 0 et 5 est bien un nombre plus grand que 1/5, donc compris entre 1/5 et + l'infini.
, donc l'image d'un nombre compris entre 0 et 5 est bien un nombre plus grand que 1/5, donc compris entre 1/5 et + l'infini.
La question subsidiaire (mais qui n'est pas posée ici) pourrait être : est-ce que tous les nombres compris entre 1/5 et + infini sont l'image d'un nombre compris entre 0 et 5 ; pourriez-vous répondre à cette question en utilisant le même raisonnement que ci-dessus ?
Par simple décroissance de la fonction inverse sur les réels strictement positifs, on a
La question subsidiaire (mais qui n'est pas posée ici) pourrait être : est-ce que tous les nombres compris entre 1/5 et + infini sont l'image d'un nombre compris entre 0 et 5 ; pourriez-vous répondre à cette question en utilisant le même raisonnement que ci-dessus ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Fonction inverse 2de
Bonjour ,
Merci pour votre réponse. Mais ce que je ne comprends pas, c’est pourquoi 1/x = + l’infini. Je ne comprends pas comment l/0 est devenu + l’infini. Je sais que ce n’est pas possible de diviser par 0 mais pourquoi le transformer en + l’infini. Pouvez me l’expliquer svp.
Merci pour votre réponse. Mais ce que je ne comprends pas, c’est pourquoi 1/x = + l’infini. Je ne comprends pas comment l/0 est devenu + l’infini. Je sais que ce n’est pas possible de diviser par 0 mais pourquoi le transformer en + l’infini. Pouvez me l’expliquer svp.
Re: Fonction inverse 2de
Bonjour,
pour ma part, pour me souvenir que 1/0 tend vers l'infini, je me dis : "qu'est-ce que ça fait si je divise 1 par un très très très petit nombre ? Par exemple 1/0,00001. Ça me donne un très très très grand nombre : 1/0,00001=100000. Donc si je divise 1 par un nombre qui tend vers 0, j'obtiens un nombre qui tend vers l'infini.
Réciproquement, si je divise1 par quelque chose de très grand qui tend vers l'infini, j'obtiens un nombre très petit qui tend vers 0.
pour ma part, pour me souvenir que 1/0 tend vers l'infini, je me dis : "qu'est-ce que ça fait si je divise 1 par un très très très petit nombre ? Par exemple 1/0,00001. Ça me donne un très très très grand nombre : 1/0,00001=100000. Donc si je divise 1 par un nombre qui tend vers 0, j'obtiens un nombre qui tend vers l'infini.
Réciproquement, si je divise1 par quelque chose de très grand qui tend vers l'infini, j'obtiens un nombre très petit qui tend vers 0.
Re: Fonction inverse 2de
On peut le voir de plusieurs façons.
Première façon : si je dis que x est plus grand que 1/5 (mais sans dire s'il est plus petit que 10 par exemple), ai-je raison de dire que x est bien dans l'intervalle [1, +infini[ ? La réponse est oui, s'il ets inférieur à 10, a plus forte raison il est "inférieur à l'infini".
Seconde façon : s'il s'agit de prouver que mon x, qui est plus grand que 1, peut vraiment aller "jusqu'à l'infini", il faut alors dire qu'il n'y a pas d'autre bornes. Donc le cas de la fonction inverse, si x est dans ]0;5[, on sait que 1/x>1/5, mais existe-t-il une borne B telle que 1/x<B ?
La réponse est négative : en effet, si je prends le nombre 1/(B+1), c'est bien un nombre compris entre 0 et 5, donc son inverse est plus grand que 5. Or son inverse est B+1, qui est strictement plus grand que B.
Donc B ne peut pas être "une borne absolue" pour l'inverse de tout nombre de l'intervalle ]0,5[.
Première façon : si je dis que x est plus grand que 1/5 (mais sans dire s'il est plus petit que 10 par exemple), ai-je raison de dire que x est bien dans l'intervalle [1, +infini[ ? La réponse est oui, s'il ets inférieur à 10, a plus forte raison il est "inférieur à l'infini".
Seconde façon : s'il s'agit de prouver que mon x, qui est plus grand que 1, peut vraiment aller "jusqu'à l'infini", il faut alors dire qu'il n'y a pas d'autre bornes. Donc le cas de la fonction inverse, si x est dans ]0;5[, on sait que 1/x>1/5, mais existe-t-il une borne B telle que 1/x<B ?
La réponse est négative : en effet, si je prends le nombre 1/(B+1), c'est bien un nombre compris entre 0 et 5, donc son inverse est plus grand que 5. Or son inverse est B+1, qui est strictement plus grand que B.
Donc B ne peut pas être "une borne absolue" pour l'inverse de tout nombre de l'intervalle ]0,5[.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
