Bonjour,
J’ai un devoir maison à faire sur la fonction exponentielle,
Sur le sujet on me donne la fonction et on m’informe que la tangente à la courbe C est horizontale (au point À d’abscisse 0),
f(x)=ae^2x+be^-x
On me demande donc la primitive,
J’en conclus sur f’(x)=2ae^2x-be^-x
Ensuite on me demande de lire graphiquement f(0) et f’(0)
f(0)=3
f ‘(0)=0
Et moi je bloque sur « En déduire de 2 équations à 2 inconnues. Calculer les valeurs de a et de b. »
Si quelqu’un pourrait m’aider ou m’éclairer, merci.
Fonction exponentielle
10 messages
- Page 1 sur 1
Re: Fonction exponentielle
Salut !
Attention, on parle d'une primitive de . Contrairement à la dérivée d'une fonction qui est unique, une fonction admet une infinité de primitive suivant la constante que l'on va rajouter. Si tu préfères, une fonction admet une unique primitive à constante additive près. Par exemple, la fonction
. Contrairement à la dérivée d'une fonction qui est unique, une fonction admet une infinité de primitive suivant la constante que l'on va rajouter. Si tu préfères, une fonction admet une unique primitive à constante additive près. Par exemple, la fonction 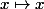 est dérivable et sa dérivée est la fonction
est dérivable et sa dérivée est la fonction 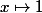 , néanmoins, toutes les fonctions de la forme
, néanmoins, toutes les fonctions de la forme  , où
, où  est une constante réelle quelconque, constituent des primitives de la fonction
est une constante réelle quelconque, constituent des primitives de la fonction 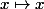 .
.
Sinon pour revenir à ton exercice, à priori je ne vois pas en quoi déterminer la dérivée de
de  t'aide à trouver une primitive
t'aide à trouver une primitive  de
de  . Je te rappelle que par définition, une primitive
. Je te rappelle que par définition, une primitive  de
de  doit vérifier
doit vérifier 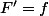 . Ici ta fonction
. Ici ta fonction  est une combinaison linéaire de deux fonctions exponentielles (de fonctions linéaires) donc tout ce que tu as besoin de connaître c'est qu'une primitive d'une combinaison linéaire de deux fonctions est une combinaison linéaire des primitive de ces deux fonctions et qu'une primitive de la fonction
est une combinaison linéaire de deux fonctions exponentielles (de fonctions linéaires) donc tout ce que tu as besoin de connaître c'est qu'une primitive d'une combinaison linéaire de deux fonctions est une combinaison linéaire des primitive de ces deux fonctions et qu'une primitive de la fonction  , où
, où  est un réel fixé, est par exemple la fonction
est un réel fixé, est par exemple la fonction  .
.
Trouver et
et  revient à résoudre le système :
revient à résoudre le système :
=3 \\ f'(0)=0<br />\end{matrix}<br />\end{cases})
On te donne la forme de l'expression) :
: = ae^{2x}+be^{-x}) , donc
, donc =a+b) .
.
Tu en as déduis la forme de l'expression : f'(x)= 2ae^{2x}- be^{-x}) , donc
, donc =2a-b) .
.
Ainsi, cela revient à résoudre le système :
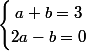
Tu as alors deux manières de procéder :
1. Soit tu raisonnes par combinaisons,
2. soit tu raisonnes par substitutions.
Attention, on parle d'une primitive de
Sinon pour revenir à ton exercice, à priori je ne vois pas en quoi déterminer la dérivée
Trouver
On te donne la forme de l'expression
Tu en as déduis la forme de l'expression
Ainsi, cela revient à résoudre le système :
Tu as alors deux manières de procéder :
1. Soit tu raisonnes par combinaisons,
2. soit tu raisonnes par substitutions.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Fonction exponentielle
De rien 
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Fonction exponentielle
J’ai un petit soucis du coup, et je me suis relu et en fait non il demandait pas la primitive mais la dérivée désolé de l’erreur.
J’ai essayé la méthode par substitution et je suis tombé à qquechose de pas cohérent: (désolé je suis sur portable donc pour utiliser l’éditeur d’équation ça va être compliqué) a+b=3 et 2a-b=0
J’ai donc ensuite fait a=3-b et donc 2(3-b)-b=0
a=3-b et 6-3b=0
-3b=-6
b=-6/3
b=-2
Et donc a=3+2=5
J’ai voulu vérifier sauf que ça colle pas, pour a+b=3 ça colle parfaitement puisque 5+(-2)=3 mais 2a-b=0 ça fait 2x5-(-2)=12
Aidez moi s’il vous plaît
J’ai essayé la méthode par substitution et je suis tombé à qquechose de pas cohérent: (désolé je suis sur portable donc pour utiliser l’éditeur d’équation ça va être compliqué) a+b=3 et 2a-b=0
J’ai donc ensuite fait a=3-b et donc 2(3-b)-b=0
a=3-b et 6-3b=0
-3b=-6
b=-6/3
b=-2
Et donc a=3+2=5
J’ai voulu vérifier sauf que ça colle pas, pour a+b=3 ça colle parfaitement puisque 5+(-2)=3 mais 2a-b=0 ça fait 2x5-(-2)=12
Aidez moi s’il vous plaît
Re: Fonction exponentielle
Mathelot c’est bien gentil d’intervenir mais s’il te plait lis moi en totalité et dans tous les cas ça n’est qd même toujours pas cohérent puisque du coup a+b=3 devient faux avec ton résultat : 5+2=7
Re: Fonction exponentielle
b vaut 2 , a vaut 1.
en écrivant b=(-6)/(-3) je t'ai indiqué où tu as fait une erreur de calcul, plus précisément une erreur de signe
dans ton post de 12h23
en écrivant b=(-6)/(-3) je t'ai indiqué où tu as fait une erreur de calcul, plus précisément une erreur de signe
dans ton post de 12h23
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
