Fonction exponentiel

[damajuma]

celle la je l'ai reussi celle que je n'est pas reussi c la 1b) et la 3b)

[mathelot]

pour la (1.b)







qu'en déduit-on pour les courbes C(f) et Delta ?

[damajuma]

justement je bloque a f(x)-1<0 je ne c pas comment la resoudre.

[mathelot]

pour la (3.b)






on dérive




f'(x) a le signe de

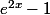
f' a le signe de (en multipliant par e^x)

[damajuma]

la formule avec laquelle tu derive c 1/u qui donne -u/u²

[laetidom]

Bjr,

1b) Position de f(x) par rapport à la droite :

C'est simple, il faut regarder le signe (+ ou -) du résultat de la différence entre l'un et l'autre :

f(x) - y = ((e(2x) -4e(x)+1) / (e(2x) + 1)) - 1 = (-4e(x)) / (e(2x) +1) ===>

numérateur 0 donc le résultat est < 0 donc Cf - < 0 donc Cf < donc que Cf est dessous la droite delta, ce que tu peux constater sur le graphe suivant : http://www.cjoint.com/c/EJClaWaj2Nf

[damajuma]

ouai c ça, je l'avais fais avec ma calculette

[damajuma]

moi j'avais essayer avec 1- (4e^x)(e^2x+1)-1 donc ça fait (-4e^x)(e^2x+1)

[damajuma]

ok g compris ;)
donc ça sert a rien de faire des équation et des inequation ?

[laetidom]

CONFIRMATION : le dénominateur de f(x) , c'est (e(2x) + 1) ou (e(2x+1)) ? . . .

? ? ? ? ? ? ? ?..................

[damajuma]

le denominateur c (e^(2x)+1)

[mathelot]

la formule avec laquelle tu derive c 1/u qui donne -u/u²

-u'/u^2

..............

[laetidom]

le denominateur c (e^(2x)+1)

OK, f ' (x) est = à quoi ?.......

[damajuma]

f'(x)= [4e^(x) * (e^(2x)-1)]/(e^(2x)+1)²

[laetidom]

f'(x)= [4e^(x) * (e^(2x)-1)]/(e^(2x)+1)²

ok c'est bon

[laetidom]

donc le signe de f ' (x) c'est le signe de e(2x) -1 puisque tout le reste est > 0, ok ?...


et e(2x) -1 s'annule pour x=......?

[laetidom]

e(2x) = 1

2x = ln 1 = 0

x=0

[damajuma]

ok le signe depend de e^(2x)-1
et pour savoir pour quelle valeur de x e^(2x)-1 s'annule il faut resoudre e^(2x)-1=0 ?

[laetidom]

3b)

donc e(2x) -1 s'annule en 0,

e(2x) -1 est 0 sur [0 ; +inf[ donc Cf croit sur le même intervalle (voir mon graphe joint)

[damajuma]

ok c bon g reussi a résoudre l'équation