Fonction dérivée / tableau de variation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 17 Oct 2010, 15:51
par chelsea-asm » 17 Oct 2010, 15:51
Bonjour,
Je suis en terminale et j'ai un peu oublié les dérivées, qu'on a vu en début d'année l'an passé.
1. Alors, j'ai une fonction :
 = x - 3 + \frac{3x-1}{x^2})
Je trouve :
 = 1 - 0 - \frac{3x^2 + 2x}{x^4})
)
 = 1 - \frac{3x + 2}{x^3})
Est-ce que j'ai juste ?
2. Après il s'agit de faire le tableau de variation... donc je cherche les valeurs où

Pour cela, si je me souviens bien, il faut trouver

et faire un tableau de signe !
Mais je n'ai pas de formule de type
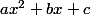
...
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Oct 2010, 15:56
par Sylviel » 17 Oct 2010, 15:56
Hum cela me semble confus... et faux.
Dans l'ordre :
la linéarité OK
par contre peux tu me rappeler ce que vaut (u/v)' ? et au passage :
u =
u' =
v =
v' =
Pour le tableau de signe, avant d'utiliser le discriminant (uniquement pour les trinomes) il y a une séparation des facteurs à faire... Rappelle toi comment on obtient le signe de A/B à partir du signe de A et du signe de B...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 17 Oct 2010, 16:04
par chelsea-asm » 17 Oct 2010, 16:04
alors (u/v)' = (u'v-v'u / v²)
et donc !
u= 3x-1
u' = 3
v= x²
v' = 2x
pour le x-3, si on dérive, x=1 et 3=0 donc cela donne 1 tout simplement !
 par eleve.ts.spémaths » 17 Oct 2010, 16:08
par eleve.ts.spémaths » 17 Oct 2010, 16:08
Salut !
Personellement quand je calcule la dérivée, je ne trouve pas la même chose que toi :
Je trouve : f'(x)= 1 + (3x-2)/(x^3)
Ensuite pour trouver le sens de variation tu dois etudier le signe de ta dérivee :
Quand la dérivée est positive, la fonction est croissante
Quand la dérivée est négative, la fonction est décroissante
Cherche donc de ce coté la ;)
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 17 Oct 2010, 16:12
par chelsea-asm » 17 Oct 2010, 16:12
Pour le tableau de signe oui je me rapelle ! Merci ;)
En revanche, j'ai dû me tromper sur les signes mais je sais pas comment je me suis débrouillé ! je trouve 1-(3x+2/x^3)
Mais je vais revérifier.
Ce qui me pose problème, c'est que pour étudier le tableau de signe. Il me faut x1 et x2 pour que la fonction dérivée soit égale à 0. Ensuite, signe de a à l'extérieur des racines si je me souviens bien.
Mais pour trouver x1 et x2 j'ai besoin de supprimer ce x^3.
Comment je dois faire ?
PS : tu es sur que je me suis trompé dans les signes ? ^^
 par eleve.ts.spémaths » 17 Oct 2010, 16:18
par eleve.ts.spémaths » 17 Oct 2010, 16:18
Je viens de recalculer et je trouve a nouveau la meme chose.
Pour l'etude du sens de variation, tu devrais faire un tableau de signe ou tu regardes le signe de (3x-2) puis celui de x^3. Ensuite le quotient des deux . Etc..
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Oct 2010, 16:24
par Sylviel » 17 Oct 2010, 16:24
(u/v)' = (u'v-v'u) / v² attention aux parenthèses !
= (3x²-2x(3x-1))/x^4
= (3x-2(3x-1))/x^3
= ...
donc f'(x)=...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 17 Oct 2010, 16:27
par chelsea-asm » 17 Oct 2010, 16:27
okay okay, donc
 = 1 + \frac{3x - 2}{x^3})
Ensuite j'étudie le signe de 3x-2 puis celui de x^3
Okay, je vais essayer, mais cependant, je dois trouver 3 variations, car en regardant ma courbe,
entre - l'infini et 0 elle monte puis redescend, et entre 0 et + l'infini, elle ne fait que de monter, 0 étant une valeur interdite!!!
Donc, je pourrais quand même trouver mes 3 flèches, en faisant cette technique ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Oct 2010, 16:55
par Sylviel » 17 Oct 2010, 16:55
Aïe aïe aïe... As tu vraiment complété mon calcul ?
ensuite c'est le signe de 1+.../... qui est important, or tu ne peux faire un tableau de signe en séparant les facteurs que si tu as des produits (ou division), pas des additions ! donc il faut tout mettre au même dénominateur.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 17 Oct 2010, 16:57
par chelsea-asm » 17 Oct 2010, 16:57
On pourrait me détailler le calcul ?
Parce que moi je trouve
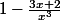
!!
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Oct 2010, 17:52
par Sylviel » 17 Oct 2010, 17:52
franchement ...
(3x-2(3x-1))/x^3
= (3x-6x+2))/x^3
= (-3x+2)/x^3
c'est de niveau 4ème ou 3ème ça...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 17 Oct 2010, 18:09
par chelsea-asm » 17 Oct 2010, 18:09
Ben ça va....
On nous casse la tete toute la journée avec toutes les matieres différentes on peut bien faire des erreurs débiles de temps en temps... des erreurs que je faisais pas en 4eme justement !
Bref,
en tous les cas, si j'étudie le signe du numérateur et le signe de x^3 et que je fais le coefficient, je trouve un tableau de variation qui correspond pas du tout à ma droite ! soit elle redescend pour un x positif, alors que la courbe descend avant 0, soit elle descend au lieu de monter...
Tant pis je demanderai à mon prof demain !
Merci de votre aide c'est simpa !
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Oct 2010, 18:16
par Sylviel » 17 Oct 2010, 18:16
Est-ce que tu lis les post en entier :id: ?
On recommence : pour étudier le signe de A/B on étudie le signe de A d'un côté, le signe de B de l'autre... et on applique la règle des signes.
Mais pour cela il faut avoir A/B et non pas 1+A/B. Donc il faut tout mettre au même dénominateur.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 17 Oct 2010, 18:21
par chelsea-asm » 17 Oct 2010, 18:21
si je mets tout au même dénominateur..
Ca me fait
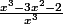
Et ça c'est peut etre du niveau de seconde... mais je ne m'en souviens plus encore malheureusement, au fur et à mesure que j'avance les choses simples je les oublies au profit des nouvelles formules :marteau:
Alors comment étudier le signe de
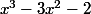
? :wrong:
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Oct 2010, 18:29
par Sylviel » 17 Oct 2010, 18:29
Non ce n'est pas évident car c'est un polynome du 3eme degré, or tu ne connais de méthode systématique que pour le second degré (Delta...)
En revanche tu peux chercher une racine évidente a et tu pourras alors factoriser par (x-a).
Courage, normalement tu devrais bientôt aboutir.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 17 Oct 2010, 18:31
par chelsea-asm » 17 Oct 2010, 18:31
"une racine évidente a" tu veux dire une racine carrée ?
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 17 Oct 2010, 18:41
par chelsea-asm » 17 Oct 2010, 18:41
Hum... j'en chie un peu !
Je trouve
)
mais je trouve pas le a pour (x-a)
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Oct 2010, 18:55
par Sylviel » 17 Oct 2010, 18:55
C'est complètement faux ce que tu as écris là...
Par ailleurs tu as encore une erreur de signe pour ton numérateur.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 17 Oct 2010, 18:55
par chelsea-asm » 17 Oct 2010, 18:55
oups !! pardon
c'est
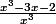
Je cherche donc le signe de
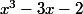
Si je factorise par x, ça me donne
)
Je suis pas doué... :hum:
Euh... apres je trouve pas le a pour factoriser par (x-a)
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Oct 2010, 18:59
par Sylviel » 17 Oct 2010, 18:59
Toujours pas ! x*\sqrt{x} ne vaut pas x... Tu ne peux factoriser par x que si 0 est une racine. Et
j'aimerais que tu me détaille ton calcul :
1+(-3x+2)/x^3= ...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 142 invités
