bonjours à tous. J'ai un certain exercice me laissant un petit rictus continue à chaque fois que je le lis.
Déterminer trois réels a, b, c tels que la courbe d'équation y= ax + b + c/(x-1) passe par A(3 ; 2) , admette en ce point une tangente horizontale et possède au point d'abscisse 2 une tangente parallèle à la droite d'équation y = 3x+2
merci d'avance de bien vouloir m'aider
Fonction dérivée 1er S
6 messages
- Page 1 sur 1
soit =ax+b+\frac{c}{x-1}) et
et  courbe représentative de
courbe représentative de )
 admet une tangente en A(3;2)
admet une tangente en A(3;2)
donc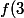=2)
on te parle ensuite d'une tangente horizontale en x=3
le fait qu'elle soit horizontale signifie que son coefficient directeur est égal à 0
d'où f'(3)=0
enfin, que cette tangente soit parallèle à une droite signifie qu'en une abscisse X, son coefficient directeur sera égal au coefficient directeur de la droite à laquelle elle est parallèle
donc
on te parle ensuite d'une tangente horizontale en x=3
le fait qu'elle soit horizontale signifie que son coefficient directeur est égal à 0
d'où f'(3)=0
enfin, que cette tangente soit parallèle à une droite signifie qu'en une abscisse X, son coefficient directeur sera égal au coefficient directeur de la droite à laquelle elle est parallèle
j'ai finalement réussi a m'en sortir en faisant un système a 2 inconnues avec f'(x) = a -(c/(x-1)²)
comme f'(3)=0 et f'(2) = 3 on a 2 équation :
a -(c/(3-1)²) = 0 et
a -(c/(2-1)²) = 3
on trouve donc a =-1 et c = -4
f(3) = ax +b + c / x-1 = 2
-3 +b -4/2 =2
b = 3 + 2 + 2 = 7
voila merci pour vos indice et signalez moi si j'ai faux :)
comme f'(3)=0 et f'(2) = 3 on a 2 équation :
a -(c/(3-1)²) = 0 et
a -(c/(2-1)²) = 3
on trouve donc a =-1 et c = -4
f(3) = ax +b + c / x-1 = 2
-3 +b -4/2 =2
b = 3 + 2 + 2 = 7
voila merci pour vos indice et signalez moi si j'ai faux :)
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
