Exponentielle

par **bbeyfashion** » 11 Oct 2006, 18:44

bonsoiiir :happy2:

voila j'ai bcp de difficulté en maths et j'ai trouver ce forum ^^

voici l'ennoncé :1f (x) = x-2 / e^x
2f (x) = x-2 + ( 1/e^x)

il faut trouver le sens de variation de la fonction mais j'ai un probleme de developpement ds la dérivée :

pour la premiere [:U]

e^x(x-1) / e^x² ==> la fonction est censée etr croissante et je n'arrive pas a justifier :cry:

[U]pour la deuxieme

1 + ( e^-x / (e^x)²)

idem je ne sais pas justifier :hum: , si vous pouvez m'aider faite moi signe !!!

merci !!!

par **fonfon** » 11 Oct 2006, 18:55

salut,

c'est quoi ça

pour la premiere [:U]

e^x(x-1) / e^x² ==> la fonction est censée etr croissante et je n'arrive pas a justifier

c'est ta derivée? et ta fonction tu l'etudie sur R tout entier ? et met des parenthéses car est-ce que

ou est-ce que c'est

par **bbeyfashion** » 11 Oct 2006, 19:10

ui c'est ma dérivée dsl pour les parenthése :

(x-2)/e^x

par **fonfon** » 11 Oct 2006, 19:25

re, je te donne la derivé que je trouve on utimise (u/v)'=(u'v-uv')/v²

petit rappel:

donc

donc apres il faut que tu etudies le signe comme e^x>0 alors f'(x) est du signe de ....

2f (x) = x-2 + ( 1/e^x)

je te donne la derivée pour la deuxieme je trouve

donc f'(x) est ....

par **bbeyfashion** » 11 Oct 2006, 19:36

ah d'accord jte remercie pour le (e^x)² j'avais oublier

pour la deuxieme la fonction graphique donne une fonction decroissante et croissante , c pour sa que en trouvant 1/ ... je ne vois pas comment justifier :doh:

par **fonfon** » 11 Oct 2006, 19:42

oui car

est croissante sur R alors que

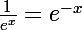
est decroissante sur R donc ici c'est à toi de voir comment vont faire tes variations avec la derivée

par **bbeyfashion** » 11 Oct 2006, 19:44

oulalala je fais le tableau de signe sa me fé du + et du - alors ke la fonction est croissante sur ] - infini ; + infini [

par **bbeyfashion** » 11 Oct 2006, 19:45

:doh: :doh: :doh: :doh:

par **bbeyfashion** » 11 Oct 2006, 19:55

pour la 1ere : f '(x)= (-x+3) / e^x

il y aurait eu les limites ca aurait été mieu pour moi , bref kes ke je doi prendre en compte pour les variation le -x+3 ou le e^x ?

par **fonfon** » 12 Oct 2006, 07:31

Re,

pour la 1ere : f '(x)= (-x+3) / e^x

il y aurait eu les limites ca aurait été mieu pour moi , bref kes ke je doi prendre en compte pour les variation le -x+3 ou le e^x ?

il faut que tu etudies le signe de (-x+3) car e^x>0 pour tt x ds R

idem pour la 2) il faut que tu mettes au même denominateur tu verras mieux donc f'(x)=(e^x-1)/e^x et que tu etudie le signe de e^x-1 car e^x >0 sur R

par **fonfon** » 12 Oct 2006, 07:33

re,

de plus tu dis que:

e^x(x-1) / e^x² ==> la fonction est censée etr croissante et je n'arrive pas a justifier

tu te fais avoir par ta calculette car ta fct est croissante puis decroissante

par **bbeyfashion** » 12 Oct 2006, 17:25

:id: merci j'ai enfin trouver =))

Exponentielle

exponentielle

re

re

encore re

...

merci

Qui est en ligne