Exponentielle et suite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
duralor
- Membre Naturel
- Messages: 26
- Enregistré le: 23 Avr 2009, 09:07
-
 par duralor » 03 Jan 2010, 11:26
par duralor » 03 Jan 2010, 11:26
Bonjour à tous. Aujourd'hui est un jour crucial : j'ai décidé de finir mon Dm de mathématiques ^^
Pour cela j'aurai besoin de votre aide :help: pour une petite question qui me pose problème:

Soit
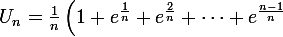)
Tout d'abord j'ai démontré que 1 + e^(1/n) + e^(2/n) + ... + e^((n-1)/n) = 1-e / 1-e^(1/n)
maintenant il faut que j'en déduise que Un = (e-1)f(1/n) et que la suite Un converge vers e-1.
On a f(x)= x/(e^(x)-1)
Merci d'avance. :++:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 03 Jan 2010, 12:09
par girdav » 03 Jan 2010, 12:09
duralor a écrit:Soit
)
Tout d'abord j'ai démontré que
/n} = 1-e / 1-e^{1/n})
maintenant il faut que j'en déduise que Un = (e-1)f(1/n) et que la suite Un converge vers e-1.
On a f(x)= x/(e^(x)-1)
Merci d'avance. :++:
Jour crucial: normal, c'est le dernier jour de vacances!
On peut calculer
\cdot f\(\fr 1n\))
pour déduire le résultat annoncé. Après, ce n'est qu'un calcul de limite classique.
-
duralor
- Membre Naturel
- Messages: 26
- Enregistré le: 23 Avr 2009, 09:07
-
 par duralor » 03 Jan 2010, 12:28
par duralor » 03 Jan 2010, 12:28
(e-1).f(1/n) = (e-1).(1/n)/(e^(1/n)-1)
= (e-1)/n / e^(1/n)-1
= n/(e-1/n) * e^(1/n)-1
= (e-1) / (e-1/n)
C'est bien cela?
-
duralor
- Membre Naturel
- Messages: 26
- Enregistré le: 23 Avr 2009, 09:07
-
 par duralor » 03 Jan 2010, 13:21
par duralor » 03 Jan 2010, 13:21
Qu'en déduire...
Un = 1/n * (1-e)/(1-e^1/n)
= (1-e) / (n-e) ?
-
duralor
- Membre Naturel
- Messages: 26
- Enregistré le: 23 Avr 2009, 09:07
-
 par duralor » 03 Jan 2010, 15:29
par duralor » 03 Jan 2010, 15:29
Up s'il vous plait :cry:
-
duralor
- Membre Naturel
- Messages: 26
- Enregistré le: 23 Avr 2009, 09:07
-
 par duralor » 03 Jan 2010, 16:05
par duralor » 03 Jan 2010, 16:05
pas beaucoup d'aide...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
