Exo sur les complexes [TS]

[dobedobedo]

Bonjour !

Je bloque sur la question suivante :

Soit le complexe ,

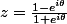
Montrer que z est un imaginaire pur



J'ai essayer de mettre z sous forme algébrique :



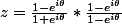
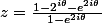
Mais ça ne m'avance pas beaucoup ...
Il y a surement un truc à faire avec [-pi; pi] mais je ne voit pas quoi :s

[Sa Majesté]

Déjà ton calcul est faux et même s'il était juste, il n'aboutirait pas à une forme algébrique de z
Il faut commencer par mettre le dénominateur sous la forme a+ib avant de multiplier numérateur et dénominateur par a-ib

Sinon une autre méthode consiste à montrer que

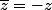
[dobedobedo]

Sinon une autre méthode consiste à montrer que

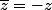
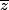
Je vois pas comment on peut exprimer avec la forme
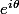
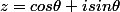
et si je passe par la forme trigonométrique , est-ce que je peut dire que ?
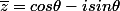
Sinon, il faudrait que je repasse par la forme algébrique, mais ce n'est pas possible si je n'ai pas la valeur de theta

[Sa Majesté]

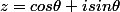
et si je passe par la forme trigonométrique , est-ce que je peut dire que ?

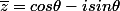
Oui

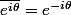
[romani01]

Salut.
On peut aussi utiliser les formules de duplication:
et

[dobedobedo]

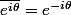
Ok merci j'ai réussi la question avec , c'est ce qu'il y avait de plus simple.
Je vais également essayer avec les formules de duplication

[Sa Majesté]

Tu as raison, il faut profiter des exercices pour tester d'autres méthodes et avoir plusieurs cordes à son arc

[Carpate]

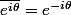
Ok merci j'ai réussi la question avec , c'est ce qu'il y avait de plus simple.
Je vais également essayer avec les formules de duplication

Une méthode plus géométrique (qui arrive un peu tardivement) :
Soient : , , ,
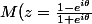Alors :, )

P décrit le cercle trigonométrique (dont AB est un diamètre),

[ft73]

en réponse au premier message, l'astuce est de factoriser en haut et en bas par exp(i*theta/2) puis appliquer les formules d'Euler.
On obtient -2i*sin(theta/2) / 2*cos(theta/2) donc -i*tan(theta/2).

A noter que theta ne peut valoir +-pi, à exclure donc de l'intervalle.

[sad13]

Bonsoir @ tous, dsl d'intervenir :

pas mal votre méthode carpate; c'est celle qu'on utilise le moins mais elle n'est pas si dure vu que ar(z)=pi/2[pi] <=> z imaginaire pur; cela dit, j'ai du mal avec la duplication et la méthode zbarre=-z car zbarre me donne : (1-(-i*téta))/(1+e(-itéta)) et -z=(e(i*téta)-1)/(1+e(i*téta)).

[Jota Be]

Salut à tous,
Je pense qu'il suffit de dire que 0 est un imaginaire pur puisque sa partie réelle est nulle.

[Carpate]

Bonsoir @ tous, dsl d'intervenir :

pas mal votre méthode carpate; c'est celle qu'on utilise le moins mais elle n'est pas si dure vu que ar(z)=+-i z imaginaire pur; cela dit, j'ai du mal avec la duplication et la méthode zbarre=-z car zbarre me donne : (1-(-i*téta))/(1+e(-itéta)) et -z=(e(i*téta)-1)/(1+e(i*téta)).

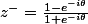
En multipliant haut et bas par

[sad13]

merci beaucoup et j'ai rectifié mon erreur à propos de l'argument, bonne soirée.

Pour la duplication, une idée pour démarrer?

[Carpate]

merci beaucoup et j'ai rectifié mon erreur à propos de l'argument, bonne soirée.

Pour la duplication, une idée pour démarrer?

Tu passe en trigonométrique :

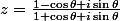
Puis :

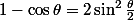
et
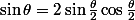
Aprés quelques factorisation et/ou simplification tu arrives à

[sad13]

ok merci ; c'est bien un imaginaire pur vu que c'est égal à un nombre réel qu'on multiplie par i.

[Carpate]

ok merci et l'argument de ce z est -pi/2+téta/2; on ne peut conclure vu téta varie.

L'argument n'intervient pas dans cette méthode !
Dans l'expression trigonométrique de z on exprime, dans les expressions que je t'ai données dans mon message précédent, théta en fonction de théta/2.
As-tu fait cela ?
Indique ton résultat si tu veux que l'on puisse t'aider.