Bonjour tout le monde j'ai un petit problème pour un exercice de Spé !!
1) Soit p un nombre premier impair.
a) Montrer qu'il existe un entier naturel k non nul tel que 2^k congru à 1 modulo P.
b) Soit k un entier naturel non nul tel que 2^k congru à 1 modulo P et soit n un entier naturel. Montrer que si k divise n alors 2^n congru à 1 modulo P.
c) Soit b tel que 2^b congru à 1 modulo P, b étant le plus petit entier naturel non nul vérifiant cette propriété.
Montrer, en utilisant la division euclidienne de n par b, que si 2^n congru à 1 modulo P alors b divise n.
2) Soit q un nombre premier impair et soit le nombre A=2^q -1. On prend pour p un facteur premier de A.
a) Justifier que 2^q congru à 1 modulo P
b) Montrer que p est impair
c) Soit b tel que 2^b congru à 1 modulo P, b étant le plus petit entier naturel non nul vérifiant cette propriété.
d) Montrer que q divise p-1, puis que p congru à 1 modulo 2q
3) soit A(1)= 217-1. Voici la liste des nombres premiers inférieurs à 400 et qui sont de la forme 34m+1, avec m entier non nul : 103,137,239,307. En déduire que A(1) est premier.
Montrer, en utilisant 1., que b divise q. En déduire que b=q
Voilà un des exercices de mon Dm que ne n'arrive pas à faire! Merci de bien vouloir m'aider !
Merci d'avance !
:++:
Exo de spé
29 messages
- Page 1 sur 2 - 1, 2
par Turn » 27 Déc 2005, 20:50
Désolé jai fait une petite erreure en recopiant que j'ai mis en gras !
Bonjour tout le monde j'ai un petit problème pour un exercice de Spé !!
1) Soit p un nombre premier impair.
a) Montrer qu'il existe un entier naturel k non nul tel que 2^k congru à 1 modulo P.
b) Soit k un entier naturel non nul tel que 2^k congru à 1 modulo P et soit n un entier naturel. Montrer que si k divise n alors 2^n congru à 1 modulo P.
c) Soit b tel que 2^b congru à 1 modulo P, b étant le plus petit entier naturel non nul vérifiant cette propriété.
Montrer, en utilisant la division euclidienne de n par b, que si 2^n congru à 1 modulo P alors b divise n.
2) Soit q un nombre premier impair et soit le nombre A=2^q -1. On prend pour p un facteur premier de A.
a) Justifier que 2^q congru à 1 modulo P
b) Montrer que p est impair
c) Soit b tel que 2^b congru à 1 modulo P, b étant le plus petit entier naturel non nul vérifiant cette propriété.
Montrer, en utilisant 1., que b divise q. En déduire que b=q
d) Montrer que q divise p-1, puis que p congru à 1 modulo 2q
3) soit A(1)= 217-1. Voici la liste des nombres premiers inférieurs à 400 et qui sont de la forme 34m+1, avec m entier non nul : 103,137,239,307. En déduire que A(1) est premier.
Voilà un des exercices de mon Dm que ne n'arrive pas à faire! Merci de bien vouloir m'aider !
Merci d'avance !
:++:
Bonjour tout le monde j'ai un petit problème pour un exercice de Spé !!
1) Soit p un nombre premier impair.
a) Montrer qu'il existe un entier naturel k non nul tel que 2^k congru à 1 modulo P.
b) Soit k un entier naturel non nul tel que 2^k congru à 1 modulo P et soit n un entier naturel. Montrer que si k divise n alors 2^n congru à 1 modulo P.
c) Soit b tel que 2^b congru à 1 modulo P, b étant le plus petit entier naturel non nul vérifiant cette propriété.
Montrer, en utilisant la division euclidienne de n par b, que si 2^n congru à 1 modulo P alors b divise n.
2) Soit q un nombre premier impair et soit le nombre A=2^q -1. On prend pour p un facteur premier de A.
a) Justifier que 2^q congru à 1 modulo P
b) Montrer que p est impair
c) Soit b tel que 2^b congru à 1 modulo P, b étant le plus petit entier naturel non nul vérifiant cette propriété.
Montrer, en utilisant 1., que b divise q. En déduire que b=q
d) Montrer que q divise p-1, puis que p congru à 1 modulo 2q
3) soit A(1)= 217-1. Voici la liste des nombres premiers inférieurs à 400 et qui sont de la forme 34m+1, avec m entier non nul : 103,137,239,307. En déduire que A(1) est premier.
Voilà un des exercices de mon Dm que ne n'arrive pas à faire! Merci de bien vouloir m'aider !
Merci d'avance !
:++:
par pianozik » 27 Déc 2005, 20:57
1) a)tu veux démontrer l'existance, vérifie pour k=2, tu obtiens ce que tu veux
b) soit p un entier premier supérieur à 3
k|n (k divise n) implique : il existe un entier h tel que
on a
[p] càd
[p]
donc
[p] et par conséquent, 
[p]
voilà pour les deux premières
b) soit p un entier premier supérieur à 3
k|n (k divise n) implique : il existe un entier h tel que
on a
[p] càd [p]donc
[p] et par conséquent, [p]voilà pour les deux premières
par Turn » 27 Déc 2005, 21:28
Pour la a j'avais fait pareil mais je sais pas si cela suffit ?? Car il dise montrer alors je sais pas si faut prendre des chiffres ou faire une démonstration !! Sinon pour la b merci ^^ !!
par pianozik » 27 Déc 2005, 21:44
Pour le a) je vois que c'est logique de vérifier pour un k, vu qu'on utilise "il existe" et non pas quelque soit. mais surement ça se démontre, mais je dis que c'est juste de vérifier, et de rien ^^
par Turn » 27 Déc 2005, 21:45
ha oki effectivement il y a aussi une analyse de mot à faire ^^ oki merci !
par pianozik » 27 Déc 2005, 21:58
les maths sont comme ça, si j'arrive à résoudre le reste je te le donnerai ^^
bon courage
bon courage
par becirj » 27 Déc 2005, 22:03
Bonsoir
La question 1.a) est en fait un cas particulier du petit théorème de Fermat qui est au programme de Term S : Si p est un entier premier et a un entier naturel non divisible par p alors)
La question 1.a) est en fait un cas particulier du petit théorème de Fermat qui est au programme de Term S : Si p est un entier premier et a un entier naturel non divisible par p alors
par Turn » 27 Déc 2005, 22:06
Ouai j'ai appris ce théorème et j'ai regardé la démonstration mais ici p est impair donc je croyais qu'il fallait faire tout un trucs avec p et ici il faut que k=p+1 or k ici est un entier naturel donc cela ne peut pas fonctionner si ??
Oki pianozik et bon film :++:
Oki pianozik et bon film :++:
par becirj » 27 Déc 2005, 22:22
Si, cela fonctionne. Prenons un exemple : p=13 , 
donc 
Pour chaque valeur de p entier différent de 2, il suffit de prendre k=p-1.
Pour chaque valeur de p entier différent de 2, il suffit de prendre k=p-1.
par becirj » 27 Déc 2005, 22:40
1.b) Soit n = kq,^q)
donc )
c) Soit n=bq+r avec
^q\times 2^r)
^q\times 2^r\equiv 1^q\times 2^r\equiv 2^r \ mod p)
Par hypothèse)
donc )
Or b est le plus petit entier naturel non nul congru à 1 modulo p et r<b , on a donc nécessairement r=0, par conséquent b divise n.
c) Soit n=bq+r avec
Par hypothèse
Or b est le plus petit entier naturel non nul congru à 1 modulo p et r<b , on a donc nécessairement r=0, par conséquent b divise n.
par Turn » 27 Déc 2005, 23:15
Pk tu prends n=bq+r ?? c'est car on dit divison euclidienne ??
Or b est le plus petit entier naturel non nul congru à 1 modulo p et r
j'ai compris sauf ton par conséquent b|n je vois pas comment t'en conclu sa avec ce qui est au dessu ^^ !!
Or b est le plus petit entier naturel non nul congru à 1 modulo p et r
j'ai compris sauf ton par conséquent b|n je vois pas comment t'en conclu sa avec ce qui est au dessu ^^ !!
par becirj » 27 Déc 2005, 23:21
Effectivement, l'égalité n=bq+r avec r<0 est la traduction de la division euclidienne de n par b, r étant le reste.
si r=0 alors n=bq et par conséquent b divise n.
si r=0 alors n=bq et par conséquent b divise n.
par Turn » 27 Déc 2005, 23:23
ha d'accord fallait revenir à l'égalité de départ oki c'est bon j'ai compris merci bcp de ton aide !! :++:
par becirj » 28 Déc 2005, 15:19
Bonjour
2.a) p est un facteur premier de A donc p divise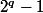
soit
. Quand on divise 
par p, le reste est 1 donc )
.
b) Supposons p pair alors kp est également pair et kp+1 est impair or
qui est pair d'où la contradiction.
Conclusion : p est impair.
c) D'après la question 1.c) b divise q, or q est premier donc b=q.
d))
d'aprés 1.a)
D'après 2.c) q est le plus petit entier congru à 1 modulo p donc d'après 1.c) q divise p-1.
On a donc
, or p étant impair, (p-1) est pair tandis que q est impair, il est donc nécessaire que a soit pair soit a=2a',on a alors
soit 
On en déduit que)
3. Je ne comprends pas la question 3, il faudrait vérifier le texte.
2.a) p est un facteur premier de A donc p divise
b) Supposons p pair alors kp est également pair et kp+1 est impair or
Conclusion : p est impair.
c) D'après la question 1.c) b divise q, or q est premier donc b=q.
d)
D'après 2.c) q est le plus petit entier congru à 1 modulo p donc d'après 1.c) q divise p-1.
On a donc
On en déduit que
3. Je ne comprends pas la question 3, il faudrait vérifier le texte.
par Turn » 28 Déc 2005, 15:45
Merci de ta réponse je vais et comprendre ce que tu as mis !! :++:
Sinon pour la 3) c'est cela :
3) soit A(1)= 2^17-1.
Voici la liste des nombres premiers inférieurs à 400 et qui sont de la forme 34m+1, avec m entier non nul : 103,137,239,307.
En déduire que A(1) est premier.
j'avais mis 217 et non 2^17 désolé !
Sinon pour la 3) c'est cela :
3) soit A(1)= 2^17-1.
Voici la liste des nombres premiers inférieurs à 400 et qui sont de la forme 34m+1, avec m entier non nul : 103,137,239,307.
En déduire que A(1) est premier.
j'avais mis 217 et non 2^17 désolé !
par Turn » 28 Déc 2005, 16:00
Tu dis que qx2a'=2qxa'
Mais si on prend q=5 et a'=4 par exemple cela ne marche pas :hein: :hein:
Mais si on prend q=5 et a'=4 par exemple cela ne marche pas :hein: :hein:
par becirj » 28 Déc 2005, 16:47
3. 
donc q=17
p est congru à 1 mod 2q soit 34 donc p=2 x 17 x m + 1=34 m+1 et par hypothèse p est premier.
donc si A admet un diviseur premier, celui-ci est inférieur à 400.
Les nombres premiers de la forme 34n+1, inférieurs à 400 sont 103, 137, 239 et 307 et on vérifie qu'aucun d'eux ne divise A, par conséquent A est premier.
Voila, c'est fini !
p est congru à 1 mod 2q soit 34 donc p=2 x 17 x m + 1=34 m+1 et par hypothèse p est premier.
Les nombres premiers de la forme 34n+1, inférieurs à 400 sont 103, 137, 239 et 307 et on vérifie qu'aucun d'eux ne divise A, par conséquent A est premier.
Voila, c'est fini !
29 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :