Exo de spé
29 messages
- Page 2 sur 2 - 1, 2
Turn a écrit: |1+i|^6 = -8i
Un module non réel!!!!
Faut résoudre Z^3 = -8i
tout exposant 6 est un exposant 3. Tu as donc une solution.
Et sinon est - il possible de tracer un cercle privé d'un point et si oui commment ??
Tu traces le cercles et tu symbolises le point exclus par un x de couleur différente ou n'importe quoi.
Il y a un problème (d'écriture ?), un module est un réel positif donc c'est ^6=-8i) et non le module.
et non le module.
Pour résoudre l'équation ,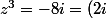^3) le plus simple est d'utiliser la forme exponentielle de z.
le plus simple est d'utiliser la forme exponentielle de z.

(-8i) a pour argument . Soit
. Soit  un argument de z,
un argument de z, =3\theta) . On doit donc avoir
. On doit donc avoir  ,
,

Ce qui donne trois complexes solutions de l'équation : ,
,  et
et  .
.
Tracer " un cercle privé d'un point" ne peut se faire qu'avec une convention : par exemple une croix sur le point à exclure.
Pour résoudre l'équation ,
(-8i) a pour argument
Ce qui donne trois complexes solutions de l'équation :
Tracer " un cercle privé d'un point" ne peut se faire qu'avec une convention : par exemple une croix sur le point à exclure.
29 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
